


Next: Eventos representables
Up: Teoría de eventos regulares
Previous: Definiciones
Contents
El conjunto de operaciones {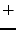 ,
, 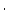 ,
, 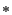 }, son llamadas operaciones regulares. Por conveniencia se utiliza el evento 0 como una operación regular nula.
}, son llamadas operaciones regulares. Por conveniencia se utiliza el evento 0 como una operación regular nula.
Las operaciones regulares satisfacen los siguientes axiomas:
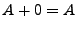
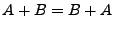
-
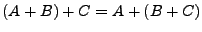
-
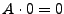
-
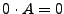
-
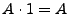
-
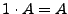
-
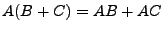
-
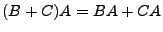
-
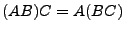
-
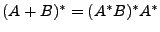
-
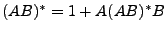
-
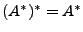
-
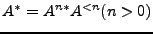
Los axiomas del 1-10 son fáciles de analizar, pero explicare los últimos 4. Primero, el axioma 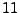 es
es
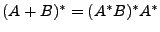 , si desarrollamos las potencias de esta expresión, obtenemos
, si desarrollamos las potencias de esta expresión, obtenemos
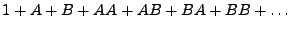 , que es la suma de todos los productos de
, que es la suma de todos los productos de  's y
's y 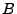 's. Del otro lado de la igualdad tenemos
's. Del otro lado de la igualdad tenemos
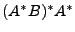 , la cual podemos expresar como
, la cual podemos expresar como
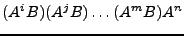 , que es el producto de 0 o más potencias de
, que es el producto de 0 o más potencias de  's particionadas por la ocurrencia de
's particionadas por la ocurrencia de 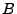 's. De manera similar tenemos que
's. De manera similar tenemos que
con lo que se demuestra el axioma 12. Para 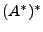 podemos ver sencillamente que
podemos ver sencillamente que
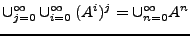 . El axioma
. El axioma 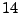 es muy parecido al
es muy parecido al 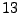 , nos dice que podemos escribir cualquier potencia de
, nos dice que podemos escribir cualquier potencia de  , digamos
, digamos 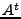 , como
, como
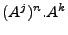 , donde
, donde 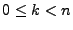 . Hay que mencionar que es común abreviar
. Hay que mencionar que es común abreviar 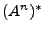 como
como 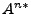 , los exponentes serán tratados como si fueran índices, así que, en adelante podríamos utilizar
, los exponentes serán tratados como si fueran índices, así que, en adelante podríamos utilizar
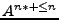 en vez de
en vez de
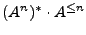 .
.
Llamaremos a un evento, regular, sólo si puede ser obtenido de los eventos 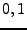 y las entradas, por medio de la aplicación repetida de las operaciones regulares {
y las entradas, por medio de la aplicación repetida de las operaciones regulares {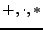 }, es decir, son un función regular de sus entradas. Al hablar acerca de un evento regular estamos hablando al mismo tiempo de un concepto tratado en la sección 2.4, una exresión regular.
}, es decir, son un función regular de sus entradas. Al hablar acerca de un evento regular estamos hablando al mismo tiempo de un concepto tratado en la sección 2.4, una exresión regular.
Ejemplo: Tomemos a
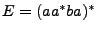 , podemos ver que es regular, ya que esta formado por los productos (posiblemente vacíos) de todas las cadenas de la forma
, podemos ver que es regular, ya que esta formado por los productos (posiblemente vacíos) de todas las cadenas de la forma
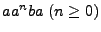 , este evento es representable, ya que el evento
, este evento es representable, ya que el evento 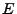 está constituido por todas las cadenas
está constituido por todas las cadenas 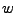 de la forma
de la forma
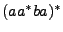 , que logran que la máquina pare en
, que logran que la máquina pare en 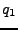 , un estado en el cual
, un estado en el cual
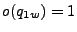 , esto es,
, esto es, 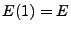 . La figura 3 muestra la representación y la tabla 3 muestra las transiciones de estados de la máquina.
. La figura 3 muestra la representación y la tabla 3 muestra las transiciones de estados de la máquina.
Figura 3:
Representación de
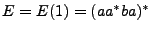 .
.
|
|
Tabla 3:
Tabla de transiciones, para la figura 3.
|
|



Next: Eventos representables
Up: Teoría de eventos regulares
Previous: Definiciones
Contents
Pablo Gerardo Padilla Beltran
2005-10-21
![]() es
es
![]() , si desarrollamos las potencias de esta expresión, obtenemos
, si desarrollamos las potencias de esta expresión, obtenemos
![]() , que es la suma de todos los productos de
, que es la suma de todos los productos de ![]() 's y
's y ![]() 's. Del otro lado de la igualdad tenemos
's. Del otro lado de la igualdad tenemos
![]() , la cual podemos expresar como
, la cual podemos expresar como
![]() , que es el producto de 0 o más potencias de
, que es el producto de 0 o más potencias de ![]() 's particionadas por la ocurrencia de
's particionadas por la ocurrencia de ![]() 's. De manera similar tenemos que
's. De manera similar tenemos que