La demostración de este teorema implica la demostración de que, la familia de las matricez cuadradas de dimensiones ![]() , forman una algebra de Kleene bajo las operaciones regulares. Esta demostración es extensa, por lo que se no se verá su totalidad en este documento, por lo que, sí el lector es interesado en examinarla, es posible encontrar dicha demostración en [JC71, cap. 3].
, forman una algebra de Kleene bajo las operaciones regulares. Esta demostración es extensa, por lo que se no se verá su totalidad en este documento, por lo que, sí el lector es interesado en examinarla, es posible encontrar dicha demostración en [JC71, cap. 3].
Conway escribió que, en cualquier máquina ![]() se define
se define
![]() como el conjunto de todas las palabras que lleven del estado
como el conjunto de todas las palabras que lleven del estado ![]() al estado
al estado ![]() . También se define
. También se define
![]() . Un evento de la matriz de transición esta definido por
. Un evento de la matriz de transición esta definido por
![]() el conjunto de entradas que lleven del estado
el conjunto de entradas que lleven del estado ![]() al estado
al estado ![]() en una sola transición.
Se usará la misma letra para representar a una máquina
en una sola transición.
Se usará la misma letra para representar a una máquina ![]() y a la matriz de transición que describe su comportamiento y cuyas entradas son eventos. Para representar un evento regular definido por
y a la matriz de transición que describe su comportamiento y cuyas entradas son eventos. Para representar un evento regular definido por ![]() , se debe definir
, se debe definir ![]() y
y ![]() como sigue:
como sigue:
![]() es un vector fila, que es el vector de entrada, el cual indica el estado inicial de la máquina, y cuyas entradas estan definidas como sigue parar el caso de una máquina binaria:
es un vector fila, que es el vector de entrada, el cual indica el estado inicial de la máquina, y cuyas entradas estan definidas como sigue parar el caso de una máquina binaria:

El vector de salida esta definido por
![]() . Las entradas de éste vector son salidas de
. Las entradas de éste vector son salidas de ![]() . En el caso en el que
. En el caso en el que ![]() es una máquina binaria(con salidas 0 ó
es una máquina binaria(con salidas 0 ó ![]() ), se pueden identificar las salidas 0 y
), se pueden identificar las salidas 0 y ![]() como los eventos 0 y
como los eventos 0 y ![]() respectivamente.
respectivamente.
De lo anterior se puede observar que
![]() , es el evento compuesto de las cadenas de longitud
, es el evento compuesto de las cadenas de longitud ![]() que llevan a
que llevan a ![]() de
de ![]() a
a ![]() , de modo que
, de modo que
![]() , es el evento de las cadenas de cualquier longitud que llevan a
, es el evento de las cadenas de cualquier longitud que llevan a ![]() de
de ![]() a
a ![]() , donde
, donde ![]() esta definida como
esta definida como
![]() , es decir, la suma infinita
, es decir, la suma infinita
![]() de las potencias de la matriz. El
de las potencias de la matriz. El ![]() representa a la matriz identidad de dimensiones
representa a la matriz identidad de dimensiones ![]() . Para poder asegurar que un evento definido por
. Para poder asegurar que un evento definido por ![]() es regular, debemos demostrar que las entradas de la matriz
es regular, debemos demostrar que las entradas de la matriz ![]() son eventos regulares, es decir, deben de ser funciones regulares de sus entradas.
son eventos regulares, es decir, deben de ser funciones regulares de sus entradas.
Conway demostró en [JC71, cap. 3], que el sistema de las matrices de dimensiones ![]() bajo las operaciones {
bajo las operaciones {![]() } es cerrado, para ello Conway [JC71] definió una Algebra de Kleene Estandard (S-algebra, Standard Kleene Algebra) como un conjunto
} es cerrado, para ello Conway [JC71] definió una Algebra de Kleene Estandard (S-algebra, Standard Kleene Algebra) como un conjunto ![]() con tres operaciones {
con tres operaciones {
![]() }(llamadas S-operaciones), definidas sobre
}(llamadas S-operaciones), definidas sobre ![]() , y elementos particulares 0 y
, y elementos particulares 0 y ![]() , de tal manera que se cumplieran las siguientes propiedades:
, de tal manera que se cumplieran las siguientes propiedades:

En ![]() ,
, ![]() indica el producto cartesiano de los conjuntos
indica el producto cartesiano de los conjuntos ![]() y
y ![]() . La suma
. La suma
![]() esta definida para todo el conjunto de índices
esta definida para todo el conjunto de índices ![]() , y denota la suma
, y denota la suma ![]() de todos los eventos de longitud
de todos los eventos de longitud ![]() siempre que
siempre que ![]() .
. ![]() denota una definición de
denota una definición de ![]() y es probable encontrarla continuamente. De lo anterior se tiene que
y es probable encontrarla continuamente. De lo anterior se tiene que
![]() .
.
Demostración.Se pueden verificar los axiomas de transitividad, de tal manera que,
![]() es cierto, entonces, si sustituimos obtenemos que
es cierto, entonces, si sustituimos obtenemos que
![]() , ya que tienen la propiedad de ser operaciones idempotentes, también se cumple que
, ya que tienen la propiedad de ser operaciones idempotentes, también se cumple que
![]() siendo
siendo ![]() el menor evento que cumple con
el menor evento que cumple con
![]() .
.
![]()
Demostración.Cualquier ![]() cumple con
cumple con
![]() , por lo tanto
, por lo tanto
![]() para cada
para cada
![]() , de donde tenemos que
, de donde tenemos que
![]() , ya que
, ya que
![]() , y sumando estas dos desigualdades para todo
, y sumando estas dos desigualdades para todo ![]() ,
se obtiene que
,
se obtiene que
![]() .
. ![]()
Para encontrar la estrella de una matriz ![]() , cuyas entradas son eventos, utilizaremos la definición de la estrella de un evento
, cuyas entradas son eventos, utilizaremos la definición de la estrella de un evento
![]() , esto es posible ya que el sistema de las matrices cuadradas es cerrado sobre las operaciones regulares.
, esto es posible ya que el sistema de las matrices cuadradas es cerrado sobre las operaciones regulares. ![]() representa la matriz identidad.
representa la matriz identidad.
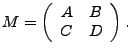

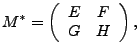
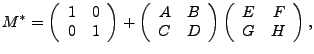
Usando el teorema 3, se deduce el siguiente sistema:
Los valores de este último sistema satisfacen las ecuaciones del primer sistema, por lo que definen una matriz ![]() , de tal manera que
, de tal manera que ![]() , cuando
, cuando ![]() .
. ![]()
Demostración.Para matrices de ![]() , esto es muy sencillo. La manera de hacerlo para matrices de
, esto es muy sencillo. La manera de hacerlo para matrices de ![]() , es igual a la forma en que se calcula la estrella de una matriz a la en el teorema 4, esto es, utilizando la definición
, es igual a la forma en que se calcula la estrella de una matriz a la en el teorema 4, esto es, utilizando la definición
![]() . Para una matriz de dimensiones
. Para una matriz de dimensiones ![]() se puede seguir el siguiente procedimiento:
se puede seguir el siguiente procedimiento:

Es posible observar que las entradas resultantes de ![]() son funciones regulares de las entradas de
son funciones regulares de las entradas de ![]() , con lo que se demuestra que
, con lo que se demuestra que ![]() es regular, y que cada una de sus entradas
es regular, y que cada una de sus entradas ![]() es una expresión regular que define un lenguaje aceptado por un autómata cuyo estado inicial es aquel definido por
es una expresión regular que define un lenguaje aceptado por un autómata cuyo estado inicial es aquel definido por ![]() y su estado final definido por
y su estado final definido por ![]() autómata.
autómata. ![]()
Hasta ahora se ha demostrado la mitad del teorema 1, y sabemos que cualquier evento representable cumple con que ![]() , para alguna máquina binaria, este evento es de la forma
, para alguna máquina binaria, este evento es de la forma ![]() y además define una expresión regular. Para la segunda parte de la demostración se analiza el hecho de que un evento
y además define una expresión regular. Para la segunda parte de la demostración se analiza el hecho de que un evento ![]() , unicamente puede ser representado por una máquina si
, unicamente puede ser representado por una máquina si
![]() , donde:
, donde:
Demostración.Podemos ver cualquier máquina como un mecanismo lineal definido por ![]() , tomando los estados de la máquina como los nodos del mecanismo, de esta manera no se afecta el evento representado por la máquina, pero para cada mecanismo lineal
, tomando los estados de la máquina como los nodos del mecanismo, de esta manera no se afecta el evento representado por la máquina, pero para cada mecanismo lineal ![]() , podemos definir una máquina cuyos estados son un subconjunto de nodos
, podemos definir una máquina cuyos estados son un subconjunto de nodos ![]() , con
, con
![]() , una función de salida
, una función de salida
![]() , sólo si existen
, sólo si existen
![]() para los cuales
para los cuales ![]() , y con estado inicial definido por conjunto de nodos
, y con estado inicial definido por conjunto de nodos ![]() en los que
en los que ![]() . La máquina tendrá
. La máquina tendrá ![]() estados si
estados si ![]() tiene
tiene ![]() nodos, y representará el mismo evento que
nodos, y representará el mismo evento que ![]() .
. ![]()
Demostración.Sabemos que
![]() , entonces
, entonces
![]() , donde
, donde
![]() define un mecanismo lineal, dado que
define un mecanismo lineal, dado que ![]() es lineal, y
es lineal, y ![]() es constante.
es constante. ![]()
Demostración.Se pueden inducir los siguientes resultados de operaciones con eventos regulares, a partir de la demostración del teorema 4, y recordando la forma descrita por el teorema anterior, ésta es, ![]() .
.
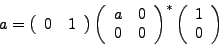

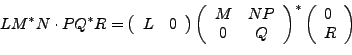
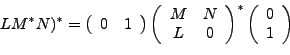
Lo anterior muestra que 0 , ![]() y las entradas (símbolos de entrada) pueden ser expresadas en la forma del teorema anterior y que si
y las entradas (símbolos de entrada) pueden ser expresadas en la forma del teorema anterior y que si ![]() y
y ![]() son eventos que cumplen con ésta característica, entonces
son eventos que cumplen con ésta característica, entonces ![]() y
y ![]() también lo harán.
también lo harán.
![]()
Como un ejemplo tomemos el evento regular
![]() , para el cual
, para el cual ![]() y
y ![]() están son representados por los diagramas de la figura 4.
están son representados por los diagramas de la figura 4.
De manera que usando la propiedad ![]() , obtenemos
, obtenemos
![$\displaystyle a^*b^*=
\left( \begin{array}{cc\vert cc}
1 & 0 & 0 & 0
\end{array...
...ght]^*
\left[ \begin{array}{c}
0 \\
0 \\
\hline
1 \\
0
\end{array}\right]
,$](img434.png)
y usando la propiedad ![]() tenemos:
tenemos:
![$\displaystyle E=
\left( \begin{array}{cccc\vert c}
0 & 0 & 0 & 0 & 1
\end{array...
...
\left[ \begin{array}{c}
0 \\
0 \\
1 \\
0\\
\hline
1
\end{array}\right]
,
$](img436.png)
Así podemos observar que ![]() es representado por el mecanismo de la figura 6(a), a partir de la cual podemos construir la máquina de la figura 6(b), omitiendo los estados inaccesibles. Como se puede observar el estado
es representado por el mecanismo de la figura 6(a), a partir de la cual podemos construir la máquina de la figura 6(b), omitiendo los estados inaccesibles. Como se puede observar el estado
![]() se repite en los tres nodos, proporciona la misma salida
se repite en los tres nodos, proporciona la misma salida ![]() en todos los casos, y cada nodo es llevado por medio de
en todos los casos, y cada nodo es llevado por medio de ![]() y
y ![]() al mismo estado, por lo que estos estados son indistinguibles y la máquina puede ser reducida a la de la figura 7.
al mismo estado, por lo que estos estados son indistinguibles y la máquina puede ser reducida a la de la figura 7.
Uno puede darse cuenta de que el mecanismo de la figura 6(a), no es un mecanismo lineal, sino un mecanismo-(constante+lineal), el cual está definido por una tupla de tres elementos ![]() , en la forma descrita por el teorema 7. En éste tipo de mecanismo, la activación de un nodo
, en la forma descrita por el teorema 7. En éste tipo de mecanismo, la activación de un nodo ![]() causa instantaneamente la activación del nodo
causa instantaneamente la activación del nodo ![]() para el cual
para el cual ![]() . Éste mecanismo-(constante+lineal) es equivalente a el mecanismo definido por
. Éste mecanismo-(constante+lineal) es equivalente a el mecanismo definido por
![]() , el cual por medio del teorema 6, es equivalente a una máquina.
, el cual por medio del teorema 6, es equivalente a una máquina.
Hasta ahora hemos podido analizar como es que éste mecanismo lineal se asemeja mucho a la máquina de Turing mencionada en las primeras secciones, ya que nos permite emular el comportamientode cualquier máquina, y en el caso de un mecanismo lineal nos deja saber como se comportan dos o más de ellas si éstas son combinadas, probablemente éste principio, de hacer interactuar dos máquinas o mecanismos conociendo unicamente sus salidas se pueda aplicar en otros contextos con resultados interesantes.
Por último, para terminar con la demostración del teorema 1 se necesita probar el siguiente teorema.
Demostración.Basta con construir dos máquinas ![]() y
y ![]() que representen a
que representen a ![]() y
y ![]() , entonces
, entonces ![]() , sólo si las versiones mínimas de
, sólo si las versiones mínimas de ![]() y
y ![]() son isomórficas, es decir, tienen el mismo comportamiento.
son isomórficas, es decir, tienen el mismo comportamiento. ![]()
Nota:
La versión mínima de una máquina ![]() es aquella máquina donde cada estado de
es aquella máquina donde cada estado de ![]() es accesible, y cada par de estados distintos son distinguibles.
es accesible, y cada par de estados distintos son distinguibles.