Se dice que una función tiene un límite A cuando ![]() tiende a
tiende a ![]()
Como vemos las condiciones mencionadas arriba para la existencia del límite se pueden interpretar de la siguiente manera: dado un disco
![]() de radio
de radio ![]() y centro en
y centro en ![]() , existen un disco
, existen un disco
![]() con centro en
con centro en ![]() y radio
y radio ![]() tal que para todo
tal que para todo ![]() en
en ![]() existe un
existe un ![]() en
en
![]() . Puede que en el centro
. Puede que en el centro ![]() no se cumpla ésto.
Hay que tomar en cuenta la definición de número complejo para poder entender los límites de funciones complejas, ya que
no se cumpla ésto.
Hay que tomar en cuenta la definición de número complejo para poder entender los límites de funciones complejas, ya que ![]() y
y ![]() son complejos. Las reglas para límites de funciones complejas son los mismos que para variable real.
son complejos. Las reglas para límites de funciones complejas son los mismos que para variable real.
Cuando aplicamos el límite estamos acercando ![]() a
a ![]() pero podemos acercarlo por muchas direcciones así que se escoge las más cómodas que son por el eje real e imaginario, es decir, un límite horizontal y un vertical. para hacer esto diremos que
pero podemos acercarlo por muchas direcciones así que se escoge las más cómodas que son por el eje real e imaginario, es decir, un límite horizontal y un vertical. para hacer esto diremos que ![]() y
y
![]() y descompondremos en límite como sigue:
y descompondremos en límite como sigue:
Si el resultado de estos dos límites es igual entonces
Para que una función sea continua en ![]() debe estar definida en
debe estar definida en ![]() y cumplir con que
y cumplir con que
La derivada de una función compleja se define como
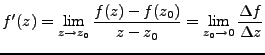
Si una función es derivable en un punto ![]() entonces es continua pero si la función es continua no implica que será derivable.
entonces es continua pero si la función es continua no implica que será derivable.
Una función se dice analítica en un punto ![]() si es continua y derivable en
si es continua y derivable en ![]() y en todo
y en todo ![]() que pertenezca a alguna vecindad de
que pertenezca a alguna vecindad de ![]() .
.
Si tenemos la función ![]() que es analítica en el punto
que es analítica en el punto ![]() y
y
![]() entonces
entonces
![]() es un coeficiente de alargamiento o contracción, dependiendo si es mayor o menor a uno. El argumento de
es un coeficiente de alargamiento o contracción, dependiendo si es mayor o menor a uno. El argumento de
![]() es igual al ángulo, al que hay que girar la tangente en
es igual al ángulo, al que hay que girar la tangente en ![]() de cualquier arco L que pasa por
de cualquier arco L que pasa por ![]() , para obtener la tangente en el punto
, para obtener la tangente en el punto
![]() a la imagen L
a la imagen L![]() de esta curva después de aplicar la transformación. Si
de esta curva después de aplicar la transformación. Si
![]() será en contra de las manecillas del reloj y viseversa.
será en contra de las manecillas del reloj y viseversa.