Transformación de Möbius

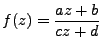
Las transformaciones de fracciones lineal o de Möbius tienen la forma general

$$f(z) = \frac{az+b}{cz+d}$$

donde $a,b,c,d$ son constantes complejas. Esta transformación es conforme en todo punto excepto donde $ad-bc = 0$ ya que en ese punto $f'(z) = 0$ y la función es constante.

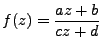
Consta de una rotación y cambio de escala, una traslación, una inversión, otra rotación y cambio de escala y otra traslación. Las propiedades de esta transformación son heredadas de las transformaciones que la conforman. Esta transformación respeta la topología de la función.

Esta transformación es uno-por-uno-e-invertible lo que significa que a cada punto en $z$ sólo le corresponderá uno en $w = f(z)$ y además despejando $z$ de la transformación podremos obtener el punto en el plano z a partir de $f(z)$. La función puede mapearse en la esfera de Riemann uno a uno y sigue siendo conforme excepto en $z = -d/c$ y $z = \infty$ ya que en estos puntos la derivada es cero o infinito.

Una de las principales propiedades de esta transformacion es que hereda la propiedad de la transformación de la inversión la cual transforma círculos o líneas en círculos o líneas, tomando en cuenta que sí tenemos un círculo en la esfera de Riemann que pasa por infinito en el plano compejo será una recta, si este círculo no pasa por el punto de fuga se transformara en un círculo.

Si modificamos la forma general de la transformación de Möbius para tenerla igualada a cero obtendremos

$$ewz + fw+gz +h = 0$$

Dados 3 puntos en el plano $z$ y otros 3 puntos en el plano $w$ que correspondan entre sí podemos saber cual es la transformación que les corresponde la cual es única. Para hacerlo haremos un sistema de ecuaciones que se puede ver desde matrices

$$\left[\begin{array}{cccc} wz & w & z & 1 \\ w_1z_1 & w_1 & z_1 & ... ...nd{array}\right] = \left[\begin{array}{c}0 \\ 0 \\ 0 \\ 0 \\ \end{array}\right]$$

Si el determinante de la matriz es igual a cero el sistema nos llevará a que la transformación esta dada por

$$\frac{w_1 - w}{w_1-w_2}\frac{w_3 - w_2}{w_3-w} = \frac{z_1 - z}{z_1-z_2}\frac{z_3 - z_2}{z_3-z}$$

Las transformaciones de Möbius tienen puntos fijos los cuales cumplen que

$$z = \frac{az+b}{cz+d}$$

Si manipulamos un poco esta ecuación tendremos que

$$cz^2 + (d-a)z-b = 0$$ (3)

Así las raíces de la ecuación serán los puntos fijos de la transformación los cuales en general serán

$$z_{+ -} = \frac{(a-d)\pm \sqrt{(a-d)^2+4cb}}{2c}$$

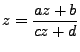
Pero cuando analizamos propiedades generales de esta transformación combiene usar una forma normalizada la cual cumple que $ad-bc = 1$, si aplicamos esta ecuación y simplificamos tendremos

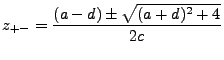$$z_{+ -} = \frac{(a-d)\pm \sqrt{(a+d)^2+4}}{2c}$$ (4)

En casos donde se estudia un caso específico de esta transformación no se ocupa la forma normalizada.

De la ecuación las transformaciones de Möbius tienen hasta dos puntos fijo, esto se cumple para todas las transformaciones menos para la identidad. Estos puntos serán únicos para cada transformación así que apartir de ellos también se puede construir la transformación.

Si se aplica la transformación a un punto fijo el resultado será el mismo punto fijo, es decir se mapea en si mismo.