Representación por matrices de la transformación de Möbius

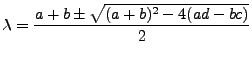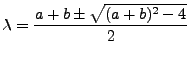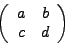
Es posible representar esta transformación a través de matrices 2x2 en la cual el determinante tiene que ser distinto de cero para que la transformación sea conforme. La matriz que representa la transformacion es la siguiente

$$\left( \begin{array}{cc} a&b \\ c&d \end{array}\right)$$

donde $a,b,c,d$ son las constantes complejas de la transformación.

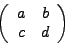
Si se quisiera aplicar una segunda iteración a la transformación ,

$$w = \frac{Az+B}{Cz+D}\ \ \ \ \ \ \ \ \ z = \frac{at+b}{ct+d}$$

$$w = \frac{A( \frac{at+b}{ct+d} )+B}{C( \frac{at+b}{ct+d})+D} = \frac{(Aa+Bc)t+Ab+Bd}{(Ca+Dc)t+Cb+Dd}$$

podríamos obtenerla de la multiplicación de las matrices de coeficientes de la transformación.

$$\left( \begin{array}{cc} A&B \\ C&D \end{array}\right) \... ...{array}{cc} Aa+Bc&Ab+Bd \\ Ca+Dc&Cb+Dd \end{array}\right)$$

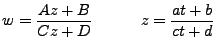
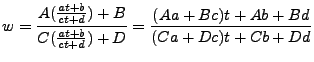
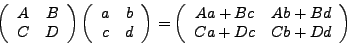
Al representar la transformación como una matriz estamos ligando nuestra transformación con el álgebra lineal, así que podemos usar algunas de sus características importantes como son los eigenvalores y los eigenvectores. Si tenemos un eigenvalor $\lambda$ y un eigenvector $\upsilon$ definido como

$$\upsilon = \left[\begin{array}{c}\upsilon_1 \\ \upsilon_2\end{array}\right]$$

únicos de la transformación cumplirán con que

$$\left[\begin{array}{cc}a & b \\ c & d\end{array}\right] \left[\be... ...ight] = \lambda\left[\begin{array}{c}\upsilon_1 \\ \upsilon_2\end{array}\right]$$

y observamos que si $z = \upsilon_1/\upsilon_2$ y le aplicamos la transformación, serán éllos mismos, así que son los puntos fijos de la transformación.

Para obtenerlos sólo usaremos el método tradicional del álgebra lineal.

$$det \left[\begin{array}{cc}a - \lambda & b \\ c & d-\lambda\end{array}\right] = 0$$

$$(a-\lambda)(d-\lambda)-bc = \lambda^2 - (a+b)\lambda +ad-bc=0$$

cuyas raíces serán

$$\lambda = \frac{a+b \pm\sqrt{(a+b)^2 - 4(ad-bc)}}{2}$$

pero como la transformación es normalizada tendremos

$$\lambda = \frac{a+b \pm\sqrt{(a+b)^2 - 4}}{2}$$