Plano de Argand

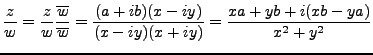
Por la definición de número complejo dicha anteriormente, suena razonable representarlo como un punto en un plano cartesiano, lo cual descubrió Argand, quien fue contemporáneo de Gauss y Leibniz quienes hicieron grandes avances en el análisis complejo.

Este plano es de coordenadas rectangulares por lo que consta de dos ejes perpendiculares entre sí, uno horizontal y otro vertical llamados eje real y eje imaginario, respectivamente. La parte real e imaginaria se representaran en su respectivo eje cada uno. La localización de los puntos es igual que en el plano euclidiano.

El punto donde se intersectan los ejes es el origen el cual representa al 0 (cero), del origen hacia la derecha y arriba son números positivos y hacia abajo y la izquierda son números negativos.

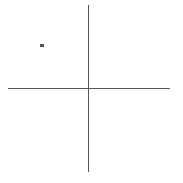
En REC/C el espacio donde se presentarán los resultados es el plano complejo (plano de Argand) por lo que podemos representar los ejes y un punto con el siguiente código:

{(
($-5.0,0.0$Gp $5.0,0.0$  g p;)[eje real]
($0.0,5.0$ Gp $0.0,-5.0$ g p;)[eje imaginario]
($-3.0,2.5$q;)[dibuja el punto]
;)}

Figura: Un número complejo es un punto en un plano

en el cual ambos ejes los dibujará de -5 a 5 y el punto será un pequeño cuadro con coordenadas (-3,2.5) que representa a $-3+2.5i$.

Podemos definir las operaciones aritméticas de una manera sencilla con esta representación.

• Suma.- la suma se define como sigue: Sea $z, w \in$ $\mathbb{C}$ y definidos como $z = a+ib$, $w = x+iy$ por lo consiguiente
  $$z+w = x+a+i(y+b)$$

• Multiplicación.- está definida así: Sea $z, w \in$ $\mathbb{C}$ y definidos como $z = a+ib$, $w = x+iy$ por lo consiguiente
  $$z*w = xa-by+i(ay+bx)$$

• División.- para definir la división de un número complejo recurriremos al conjugado para eliminar la unidad imaginaria del denominador. Sea $z, w \in$ $\mathbb{C}$ y definidos como $z = a+ib$, $w = x+iy$ por lo consiguiente
  $$\frac z w = \frac z w \frac {\overline w} {\overline w} = \frac{(a+ib) (x-iy)}{(x-iy)(x+iy)} = \frac{xa+yb+i(xb-ya)}{x^2+y^2}$$