Representación vectorial

La representación vectorial es también muy utilizada ya que al representar un número complejo como un vector hereda propiedades y herramientas del análisis vectorial.

Para representar un número complejo como un vector (segmento de recta dirigido) se localiza el punto en el diagrama de Argand y el vector se conformará del origen al punto previamente localizado.

Las características de las operaciones con vectores respetan a las de los números complejos e incluso las describen de tal manera que muchas demostraciones son más simples de hacer y entender por una representación de este tipo.

La representación geométrica de una suma compleja es una suma vectorial y se demuestra la conmutatividad con la ley del paralelogramo. A continuación la representación de una suma compleja con REC/C.

{(
($-5.0,0.0$Gp $5.0,0.0$  g p;)[eje real]
($0.0,5.0$ Gp $0.0,-5.0$ g p;)[eje imaginario]
(Z G p $2.0,1.5$g   Z G p $-1.0,2$g + G Z g p;)
;)}

Figura: Una suma vectorial es una suma compleja

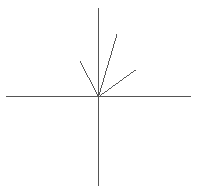
En esta figura se muestran los vectores correspondientes a los números complejos $2+1.5i$ y $-1+2i$ así como el vector resultante de su suma.

Podemos demostrar la conmutatividad de la suma con la ley del paralelogramo de análisis vectorial con una representación en REC/C

{(
($-5.0,0.0$Gp $5.0,0.0$  g p;)[eje real]
($0.0,5.0$ Gp $0.0,-5.0$ g p;)[eje imaginario]
(QR Z G p $2.0,1.5$g QB G  $-1.0,2.0$ + g QG G Zgp  p;)[parte derecha]
(QB Z G p $-1.0,2.0$g QR G $2.0,1.5$+g p  ;)[parte izquierda]
;)}

Figura: Ley del paralelogramo

Recordemos que los vectores tienen asociada una magnitud o módulo lo cual es la longitud de dicho vector, dicha unidad es un escalar. El módulo de $z = x+iy$ es denotado por $\vert z\vert$ y definido como

$$\vert z\vert = \sqrt{x^2+y^2}$$

Si notamos que $z\overline z = x^2+y^2$ podremos definir que $z\overline z = \vert z\vert^2$