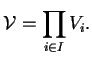 |
(4) |
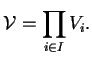 |
(4) |
denota el conjunto de todos los mapeos
![]() tal que
tal que
![]() para cada
para cada ![]() .
.
Bajo esta construcción,
![]() se denota como el producto directo o producto cartesiano de los espacios
se denota como el producto directo o producto cartesiano de los espacios
![]() . El producto cartesiano es una de las maneras más sencillas de fomar un espacio vectorial complicado utilizando espacios más simples [McI99]. Las funciones que vayan desde las bases a los elementos del producto se denominan proyecciones y sirven para recobrar los factores originales del producto cartesiano.
. El producto cartesiano es una de las maneras más sencillas de fomar un espacio vectorial complicado utilizando espacios más simples [McI99]. Las funciones que vayan desde las bases a los elementos del producto se denominan proyecciones y sirven para recobrar los factores originales del producto cartesiano.