Espacios Métricos

Sea $\mathcal{C}$ un conjunto, suponga que existe una función real $d$ para los pares ordenados $(\mathrm{C}_{i},\mathrm{C}_{j}) \in \mathcal{C}\times \mathcal{C}$ tal que satisface:

1. $d(\mathrm{C}_{i},\mathrm{C}_{j})\geq 0$     $\forall$     $\mathrm{C}_{i},\mathrm{C}_{j} \in \mathcal{C}$.
2. $d(\mathrm{C}_{i},\mathrm{C}_{j})= 0 \Leftrightarrow \mathrm{C}_{i} = \mathrm{C}_{j}$.
3. $d(\mathrm{C}_{i},\mathrm{C}_{j})= d(\mathrm{C}_{j},\mathrm{C}_{i})$.
4. $d(\mathrm{C}_{i},\mathrm{C}_{k})\leq d(\mathrm{C}_{i},\mathrm{C}_{j})+ d(\mathrm{C}_{j},\mathrm{C}_{k})$ (desigualdad
   triangular).

Entonces $\mathcal{C}$ es un espacio métrico y $d$ una distancia o métrica sobre $\mathcal{C}$ [Hal50].

Para el conjunto de estados $K$ de un autómata celular lineal, podemos formar el conjunto $\mathcal{C}$ de todas las posibles configuraciones de estados, cada configuración infinita en ambas direcciones. Entonces $\mathcal{C}$ consiste en el producto cartesiano de $K$ indexado por el conjunto de todos los enteros $\mathbb{Z}$ o también:

$$\mathcal{C}= K^{\mathbb{Z}}.$$ (5)

lo que indica la formación del producto cartesiano con un solo conjunto, en este caso $K$. Para la $i$-ésima configuración $\mathrm{C}_{i} \in \mathcal{C}$, se utilizarán las siguientes convenciones.

• $\mathrm{C}_{i[a]}$ será la célula ubicada en la posición $a$ en la configuración $\mathrm{C}_{i}$, para $a \in Z$.
• $\mathrm{C}_{i[a \ldots b]}$ será la secuencia de estados contenida en la configuración $\mathrm{C}_{i}$ que cuyo intervalo empieza en la posición $a$ y termina en la posición $b$ para $a,b \in \mathbb{Z}$ con $a \leq b$.
• La longitud de la secuencia $\mathrm{C}_{i[a \ldots b]}$ está dada por $b-a+1$.

En base al trabajo de Hedlund en [Hed69] y de Mike Boyle en [Boy93], sobre cada par ordenado $(\mathrm{C}_{i},\mathrm{C}_{j}) \in \mathcal{C}\times \mathcal{C}$ con $\mathrm{C}_{i},\mathrm{C}_{j} \in \mathcal{C}$, definamos la función $d(\mathrm{C}_{i},\mathrm{C}_{j})$ de la siguiente manera:

$$d(\mathrm{C}_{i},\mathrm{C}_{j})= \left\{ \begin{array}{ll} 0 & \... ...\mbox{ \'o } \mathrm{C}_{i[-r]} \neq \mathrm{C}_{j[-r]}. \end{array} \right.$$ (6)

Entonces $d(\mathrm{C}_{i},\mathrm{C}_{j})=(1+r)^{-1}$ define una métrica sobre el conjnto de configuraciones infinitas $\mathcal{C}$ de un autómata celular lineal, esto es ya que:

a)

$d(\mathrm{C}_{i},\mathrm{C}_{j})=(1+r)^{-1}$ es una función real que toma valores en el intervalo $[0,1]$ pues:

$d(\mathrm{C}_{i},\mathrm{C}_{j})=0$ si $\mathrm{C}_{i}=\mathrm{C}_{j}$.

$d(\mathrm{C}_{i},\mathrm{C}_{j})=1$ si $\mathrm{C}_{i[0]} \neq \mathrm{C}_{j[0]}$.

$(1+r)^{-1}\rightarrow 0$    cuando $r \rightarrow \infty$.

b)

$d(\mathrm{C}_{i},\mathrm{C}_{j})=(1+r)^{-1}$ significa que $\mathrm{C}_{i[-r \ldots r]} \neq \mathrm{C}_{j[-r \ldots r]}$ lo que implica también que $d(\mathrm{C}_{j},\mathrm{C}_{i})= (1+r)^{-1}$.

c)

Sea $d(\mathrm{C}_{i},\mathrm{C}_{j})=(1+r_1)^{-1}$ y $d(\mathrm{C}_{j},\mathrm{C}_{k})=(1+r_2)^{-1}$; tomemos a $m=\min\{r_1,r_2\}$, entonces:

$$d(\mathrm{C}_{i},\mathrm{C}_{k})\leq (1+m)^{-1} \leq (1+r_1)^{-1} + (1+r_2)^{-1}$$

$$= d(\mathrm{C}_{i},\mathrm{C}_{j})+ d(\mathrm{C}_{j},\mathrm{C}_{k})$$

cumpliendo con la desigualdad triangular.

Figura 6: Distancia $r_1$ entre $\mathrm{C}_{i}$ y $\mathrm{C}_{k}$.

Por lo que $d(\mathrm{C}_{i},\mathrm{C}_{j})=(1+r)^{-1}$ define un distancia sobre $\mathcal{C}$; por ejemplo, para un autómata celular lineal con $k=2$, tres configuraciones posibles son:

Configuración	Posiciones
	$\ldots$	-3	-2	-1	0	1	2	3	$\ldots$
$\mathrm{C}_{1}$	$\ldots$	0	0	0	1	0	0	0	$\ldots$
$\mathrm{C}_{2}$	$\ldots$	1	0	0	1	0	0	0	$\ldots$
$\mathrm{C}_{3}$	$\ldots$	0	0	0	1	0	1	0	$\ldots$

En este caso se tiene que:

$$\begin{array}{c} d(\mathrm{C}_{1},\mathrm{C}_{2})=d(\mathrm{... ...3})=d(\mathrm{C}_{3},\mathrm{C}_{1})=(1+2)^{-1}=1/3 \end{array}$$

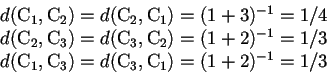
cumpliendo con la desigualdad triangular pues $d(\mathrm{C}_{1},\mathrm{C}_{3}) < d(\mathrm{C}_{1},\mathrm{C}_{2}) + d(\mathrm{C}_{2},\mathrm{C}_{3})$.

Por supuesto, otro tipo de métricas son posibles, como la expuesta por Douglas Lind y Brian Marcus en [LM95] que tiene la siguiente forma:

$$d(\mathrm{C}_{i},\mathrm{C}_{j})= \left\{ \begin{array}{ll} 0 & \... ...athrm{C}_{i[-r \ldots r]} = \mathrm{C}_{j[-r \ldots r]}. \end{array} \right.$$ (7)

En ambos casos, las métricas toman en cuenta que las configuraciones $\mathrm{C}_{i}$ y $\mathrm{C}_{j}$ concuerden en una parte central, en donde la especificación del centro es arbitraria por lo que dos configuraciones pueden estar muy cercanas o no dependiendo donde se defina el centro. Una generali-zación de ambas distancias puede realizarse tomando a $(n+r)^{-1}$ ó a $(n)^{-r}$ donde $n \in \mathbb{Z}^+$.

¿Puede entonces existir una distancia que sólo indique cuanto difiere una configuración de otra sin importar el lugar donde se presenten las diferencias?; para esto definamos la siguiente métrica:

$$\delta_r(\mathrm{C}_{i},\mathrm{C}_{j})= \left\{ \begin{array}{ll... ... 0 & \mbox{si } \mathrm{C}_{i[r]} = \mathrm{C}_{j[r]}. \end{array} \right.$$ (8)

entonces

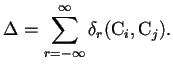$$\Delta=\sum_{r=-\infty}^{\infty} \delta_{r}(\mathrm{C}_{i},\mathrm{C}_{j}).$$ (9)

La métrica se definirá como:

$$d(\mathrm{C}_{i},\mathrm{C}_{j})=1-2^{-\Delta}.$$ (10)

Para este caso, si $\mathrm{C}_{i}=\mathrm{C}_{j}$ entonces $\Delta=0$ y $d(\mathrm{C}_{i},\mathrm{C}_{j})=1-2^{0}=0$; si $\Delta=n$ para $n \in \mathbb{Z}^+$, entonces $d(\mathrm{C}_{i},\mathrm{C}_{j})=1-2^{-n}$. Así, la distancia $d(\mathrm{C}_{i},\mathrm{C}_{j})=1-2^{-\Delta} \rightarrow 1$ conforme $\Delta \rightarrow \infty$ de ahí que $d(\mathrm{C}_{i},\mathrm{C}_{j})$ se encuentre en el intervalo $[0,1)$, con la diferencia que esta distancia se concentra en medir diferencias entre configuraciones en vez de similitudes entre partes centrales. En la continuación de este trabajo utilizaremos la distancia definida por Hedlund en [Hed69]; es decir, $d(\mathrm{C}_{i},\mathrm{C}_{j})=(1+r)^{-1}$.