Conjuntos Abiertos en $\mathcal{C}$

La definición de conjuntos abiertos en el espacio de configuraciones $\mathcal{C}$ de un autómata celular lineal es sencilla al utilizar el concepto de distancia. Para $m \in \mathbb{R}^+$ y $\mathrm{C}_{i} \in \mathcal{C}$, definimos el subconjunto $\mathrm{B}_m{(\mathrm{C}_{i})}=\{ \mathrm{C}_{j} \in \mathcal{C}: d(\mathrm{C}_{i},\mathrm{C}_{j})< m \}$; es decir, $\mathrm{B}_m{(\mathrm{C}_{i})}$ es el subconjunto de configuraciones que están a una distancia menor que $m$ de $\mathrm{C}_{i}$. A dicho subconjunto se le denomina un disco abierto de radio $m$, para el caso donde $d(\mathrm{C}_{i},\mathrm{C}_{j})\leq m$ el subconjunto se denomina un disco cerrado y se denota con $\overline{\mathrm{B}_m{(\mathrm{C}_{i})}}$.

Sea $\mathcal{F}$ la familia de subconjuntos de $\mathcal{C}$ tal que para cada $\mathrm{F}\in \mathcal{F}$, si $\mathrm{C}_{i} \in \mathrm{F}$ entonces existe $m \in \mathbb{R}^+$ tal que $\mathrm{B}_m{(\mathrm{C}_{i})} \subset \mathrm{F}$; de este modo, la familia $\mathcal{F}$ define una topología formada por los conjuntos abiertos $\mathrm{F}$ y $\mathcal{C}$ se dice un espacio topológico métrico o simplemente un espacio métrico.

Para un autómata celular lineal con $k=2$, tomemos solamente las configuraciones de tamaño $2$.

Tabla 1: Configuraciones formadas con 2 estados de longitud 2

Conjunto $\mathcal{C}$

00

01

10

11

Tomando a $d(\mathrm{C}_{i},\mathrm{C}_{j})=(1+r)^{-1}$ se obtiene que los discos cerrados son:

Tabla: Esferas cerradas de $\mathcal{C}$

$\mathrm{C}\in \mathcal{C}$	$m$	$\overline{\mathrm{B}_m{(\mathrm{C})}}$
	0	00
00	1/2	01
	1	10,11
	0	01
01	1/2	00
	1	10,11
	0	10
10	1/2	11
	1	00,01
	0	11
11	1/2	10
	1	00,01

Propongamos a

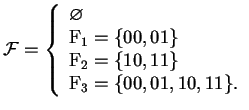$$\mathcal{F}= \left\{ \begin{array}{l} \varnothing \mathrm{F}_{... ...thrm{F}_{2}=\{10,11\} \mathrm{F}_{3}=\{00,01,10,11\}. \end{array} \right.$$ (11)

Para $\mathrm{F}_{1}$, se observa que los discos abiertos son:

$$\begin{array}{l} \mathrm{B}_{1/2}{(00)}=\{00\} \in \mathrm{F... ...thrm{B}_{1}{(00)}=\{00,01\} \in \mathrm{F}_{1}. \\ \end{array}$$

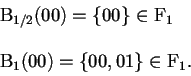
el mismo caso se presenta para $\mathrm{F}_{2}$ y $\mathrm{F}_{3}$, además, se cumple que:

$$\begin{array}{l} \mathrm{F}_{1} \cup \mathrm{F}_{2} = \mathr... ... \mathrm{F}_{3} \cap \varnothing = \varnothing. \\ \end{array}$$

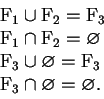
lo que muestra que $\mathcal{F}$ define una topología sobre $\mathcal{C}$, en el ejemplo, el conjunto de configuraciones de longitud $2$.

Es posible observar en el ejemplo anterior que si sólo formamos a $\mathcal{F}$ con el conjunto vacío y el conjunto total cumplirán con ser conjuntos abiertos y también sus uniones e intersecciones caen dentro de $\mathcal{F}$, siendo $\mathcal{F}=\{ \varnothing, \mathcal{C}\}$ la topología discreta de $\mathcal{C}$ como se definió en la sección 3.2. Teniendo estos resultados, podemos ver que $d(\mathrm{C}_{i},\mathrm{C}_{j})=(1+r)^{-1}$ induce una topología sobre el espacio de configuraciones $\mathcal{C}$ de un autómata celular lineal.