




Next: Conjuntos de Cilindros
Up: Propiedades del Espacio Métrico
Previous: Propiedades del Espacio Métrico
Contenido
Indice
Para el espacio de configuraciones
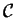 , se dirá que una configuración
, se dirá que una configuración
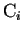 converge a
converge a
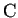 si
si
![$ d(\mathrm{C}_{i[-r \ldots r]},\mathrm{C}) \rightarrow 0$](img187.gif) conforme
conforme
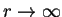 ; es decir:
; es decir:
![$\displaystyle \lim_{r \rightarrow \infty}{\mathrm{C}_{i[-r \ldots r]}}=\mathrm{C}.$](img188.gif) |
(14) |
Supongamos que
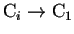 y
y
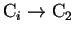 , entonces
, entonces
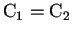 ; esto se puede probar utilizando la desigualdad del triángulo.
; esto se puede probar utilizando la desigualdad del triángulo.
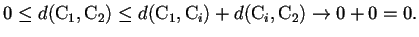 |
(15) |
Así
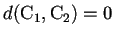 por lo que
por lo que
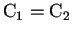 , mostrando que el límite es único.
, mostrando que el límite es único.
ice
2001-08-30
![]() y
y
![]() , entonces
, entonces
![]() ; esto se puede probar utilizando la desigualdad del triángulo.
; esto se puede probar utilizando la desigualdad del triángulo.
![]() por lo que
por lo que
![]() , mostrando que el límite es único.
, mostrando que el límite es único.