Topología Básica de los Autómatas Celulares Lineales Reversibles

Se ha observado que en el espacio de configuraciones $\mathcal{C}$ de un autómata celular lineal se puede inducir una métrica con la elección arbitraria de un centro, la cual nos permite definir conjuntos abiertos y topologizar a $\mathcal{C}$. Un tipo especial de conjuntos abiertos son los cilindros, con los cuales podemos caracterizar a $\mathcal{C}$ como compacto y separable del tipo de un espacio de Hausdorff. En un autómata celular lineal reversible, encontraremos además que toda secuencia de configuraciones que se van generando en la evolución del mismo tendrán una métrica periódica si las configuraciones son de longitud finita, pues dado que el número de posibilidades está res-tringido, una configuración tendrá que repetirse tarde o temprano, dicha configuración debe ser la inicial pues de otro modo el autómata no cumple con ser reversible.

Dado que en un autómata reversible no existe el Jardín del Edén, toda configuración es posible de formarse, por lo que este tipo de autómatas caen en la categoría de corrimientos completos, es decir, en un autómata celular lineal reversible se tiene que:

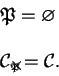$$\begin{array}{l} \mathfrak{P}= \varnothing \mathcal{C}_... ...{\mbox{\small$\times$}} \end{picture}}=\mathcal{C}. \end{array}$$ (35)