Como se vió en la sección anterior, la obtención de la cuantización
de ![]() y la componente
y la componente ![]() del momento angular debe
basarse en argumentos un poco menos directos que los usados. La
dificultad de los argumentos empleados es un problema que se
tienen desde el trabajo original de Dirac [6] y ha sido la
causa de diversos trabajos al respecto [65,66], pues es de
importancia fundamental aclarar las bases de la cuantización de
del momento angular debe
basarse en argumentos un poco menos directos que los usados. La
dificultad de los argumentos empleados es un problema que se
tienen desde el trabajo original de Dirac [6] y ha sido la
causa de diversos trabajos al respecto [65,66], pues es de
importancia fundamental aclarar las bases de la cuantización de
![]() .
.
![]() tiene la forma (sección I.B):
tiene la forma (sección I.B):
| (1) |
o sea, es el producto de una carga eléctrica por una
magnética, dividido entre la velocidad de la luz. El resultado
de que
![]() pueda
tomar sólo valores enteros (o semienteros) implica,
conociendo experimentalmente la cuantización de la carga
eléctrica, que la carga magnética, de existir, está
también cuantizada. Esta es una situación única en la
física; el tener que de las condiciones primarias de una
teoría (la Mecánica Cuántica), se obtengan condiciones
conclusivas sobre un posible observable fundamental. Siendo este
resultado teóricamente tan satisfactorio, la no existencia de
partículas cargadas magnéticamente, de ser verdadera, debe
ser efecto de profundos requerimientos de alguna teoría más
básica que la Mecánica Cuántica. Ha habido la especulación
de que el problema de la cuantización de la carga magnética
está estrechamente ligado con el del valor exacto de la
constante de estructura fina
pueda
tomar sólo valores enteros (o semienteros) implica,
conociendo experimentalmente la cuantización de la carga
eléctrica, que la carga magnética, de existir, está
también cuantizada. Esta es una situación única en la
física; el tener que de las condiciones primarias de una
teoría (la Mecánica Cuántica), se obtengan condiciones
conclusivas sobre un posible observable fundamental. Siendo este
resultado teóricamente tan satisfactorio, la no existencia de
partículas cargadas magnéticamente, de ser verdadera, debe
ser efecto de profundos requerimientos de alguna teoría más
básica que la Mecánica Cuántica. Ha habido la especulación
de que el problema de la cuantización de la carga magnética
está estrechamente ligado con el del valor exacto de la
constante de estructura fina ![]() :
:
| (2) |
siendo el último resultado en la ec. (2), experimental. La analogía de esta cantidad con:
| (3) |
En el trabajo original de Dirac [6]; se obtiene la cuantización
de ![]() del estudio de los cambios de
fase físicamente aceptables de las funciones de onda
(aquellos que no dan lugar a ambigüedades en la
interpretación de la teoría cuántica) cuando se estudia
su comportamiento sobre una curva cerrada que rodea una línea
en la cual una de estas funciones es O (estas líneas en las
cuales se anulan las funciones de onda se denominan líneas
nodales; trabajando no con 3 dimensiones
del estudio de los cambios de
fase físicamente aceptables de las funciones de onda
(aquellos que no dan lugar a ambigüedades en la
interpretación de la teoría cuántica) cuando se estudia
su comportamiento sobre una curva cerrada que rodea una línea
en la cual una de estas funciones es O (estas líneas en las
cuales se anulan las funciones de onda se denominan líneas
nodales; trabajando no con 3 dimensiones ![]() sino con 4
sino con 4
![]() , se obtienen superficies nodales). Los cambios
de fase deben, entonces, para evitar ambigüedades de
interpretación, estar cuantizados de tal manera que, de acuerdo
a los argumentos de Dirac,
, se obtienen superficies nodales). Los cambios
de fase deben, entonces, para evitar ambigüedades de
interpretación, estar cuantizados de tal manera que, de acuerdo
a los argumentos de Dirac,
![]() debe ser igual
a un entero.
debe ser igual
a un entero.
Posteriormente, en 1944, Fierz [65] obtuvo el mismo resultado usando
otro método, el cual se basa en el requerimiento de que las
funciones de onda aceptables formen parte de un espacio de
representación del grupo de rotaciones ![]() ; el requerimento
realmente esencial consiste en que las funciones de onda deben ser
cuadráticamente integrables (elementos de un espacio de
Hilbert), el cual proviene directamente de los postulados de la
Mecánica Cuántica [68]. Recientemente Hurst [66]
ha seguido un procedimiento análogo al de Fierz, pero desde un
punto de vista más algebraico; en su trabajo, Hurst menciona la
manera en que el problema de la cuantización de
; el requerimento
realmente esencial consiste en que las funciones de onda deben ser
cuadráticamente integrables (elementos de un espacio de
Hilbert), el cual proviene directamente de los postulados de la
Mecánica Cuántica [68]. Recientemente Hurst [66]
ha seguido un procedimiento análogo al de Fierz, pero desde un
punto de vista más algebraico; en su trabajo, Hurst menciona la
manera en que el problema de la cuantización de
![]() está ligado con el de las condiciones bajo las
cuales un álgebra de Lie se puede integrar para obtener el grupo
de Lie correspondiente. Se describen a continuación los
métodos de Fierz y Hurst con los pormenores relevantes; dicha
descripción se basa en uso de coordenadas esféricas
está ligado con el de las condiciones bajo las
cuales un álgebra de Lie se puede integrar para obtener el grupo
de Lie correspondiente. Se describen a continuación los
métodos de Fierz y Hurst con los pormenores relevantes; dicha
descripción se basa en uso de coordenadas esféricas
![]() (las mismas que usaron ellos) por razones
que se explican al final de la parte concerniente al trabajo de
Fierz.
(las mismas que usaron ellos) por razones
que se explican al final de la parte concerniente al trabajo de
Fierz.
i) Procedimento de Fierz. Escribiendo la solución para la
coordenada ![]() en la forma:
en la forma:
| (4) |
| (5) |
El argumento se basa en la observación de que la observable representada por el operador siguiente es una constante del movimiento:
| (6) |
(
![]() es el análogo cuántico del
vector
es el análogo cuántico del
vector ![]() de ``momentum angular total", cuya constancia
en el caso clásico se demostró en las secciónes I.B y I.C.
de ``momentum angular total", cuya constancia
en el caso clásico se demostró en las secciónes I.B y I.C.
![]() está dado por (ec. 7, sección I.B):
está dado por (ec. 7, sección I.B):
![]() ).
Las cantidades que aparecen en la ec. (6) representan realmente
operadores, pero se usará la notación del caso clásico
mientras no haya confusiones. La constancia de
).
Las cantidades que aparecen en la ec. (6) representan realmente
operadores, pero se usará la notación del caso clásico
mientras no haya confusiones. La constancia de
![]() se demuestra más adelante, en la
sección II.D.
se demuestra más adelante, en la
sección II.D.
Además, como se verá en la sección II.D, las componentes de
![]() satisfacen las relaciones de conmutación
(análogas a las de paréntesis de Poisson del caso clásico,
ec. (179), sección I.C):
satisfacen las relaciones de conmutación
(análogas a las de paréntesis de Poisson del caso clásico,
ec. (179), sección I.C):
| (7) |
Las relaciones anteriores corresponden a las de el Álgebra de Lie
de los generadores del grupo ![]() , o sea, son las relaciones comúnmente
llamados de momentum angular. Siguiendo el procedimiento de rutina para
el momento angular [69], se definen ahora los operadores de escalera dados por:
, o sea, son las relaciones comúnmente
llamados de momentum angular. Siguiendo el procedimiento de rutina para
el momento angular [69], se definen ahora los operadores de escalera dados por:
| (8) |
| (9) |
Se puede escribir, en coordenadas esféricas [65]:
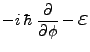 |
(10) | ||
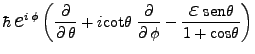 |
(11) | ||
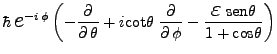 |
(12) |
En las ecuaciones anteriores, ![]()
![]() ,
de acuerdo con la sección I.B. Ahora, se encontrará un conjunto de funciones que son
eigenfunciones de
,
de acuerdo con la sección I.B. Ahora, se encontrará un conjunto de funciones que son
eigenfunciones de
![]() y que forman un espacio que es base para una
representación de
y que forman un espacio que es base para una
representación de ![]() . Es claro que estas eigenfunciones pueden escogerse
como funciones de onda (eigenfunciones del Hamiltoniano
. Es claro que estas eigenfunciones pueden escogerse
como funciones de onda (eigenfunciones del Hamiltoniano ![]() ) pues
) pues
![]() y
y ![]() conmutan:
conmutan:
![]() . Pero,
de acuerdo con los postulados de la Mecánica Cuántica [68], las
eigenfunciones de
. Pero,
de acuerdo con los postulados de la Mecánica Cuántica [68], las
eigenfunciones de ![]() deben ser cuadráticamente integrables; como se mencionó
anteriormente, éste es el requerimiento esencial, del cual se implica la
cuantización buscada.
deben ser cuadráticamente integrables; como se mencionó
anteriormente, éste es el requerimiento esencial, del cual se implica la
cuantización buscada.
Se debe tener, entonces, que las eigenfunciones ![]() de
de
![]() (que lo son, de acuerdo con lo anterior, de
(que lo son, de acuerdo con lo anterior, de ![]() ) satisfacen la condición:
) satisfacen la condición:
| (13) |
Si se describen las funciones de onda en la forma:
| (14) |
| (15) |
Usando ahora la ecuación (de comprobación trivial desarrollando el lado derecho):
| (16) |
| (17) |
Usando ahora ![]() , se obtiene una fórmula que tiene a
, se obtiene una fórmula que tiene a ![]() en el lado izquierdo. Por aplicación repetida de estas dos
fórmulas se obtiene:
en el lado izquierdo. Por aplicación repetida de estas dos
fórmulas se obtiene:
| (18) |
| (19) |
En términos de
![]() , la expresión (13) se convierte en:
, la expresión (13) se convierte en:
| (20) |
En general, si los términos encerrados por los corchetes de las ecs.
(18,19) contienen potencias de ![]() que no son números
enteros positivos; por aplicación del operador de derivada, a
medida que
que no son números
enteros positivos; por aplicación del operador de derivada, a
medida que ![]() crece se tendrá que
crece se tendrá que ![]() y
y ![]() contienen potencias de
contienen potencias de ![]() negativas con módulos arbitrariamente
grandes; o sea para cada
negativas con módulos arbitrariamente
grandes; o sea para cada ![]() , existirá un valor de
, existirá un valor de ![]() a partir
del cual la condición (20) no se cumple para
a partir
del cual la condición (20) no se cumple para ![]() y
y ![]() , por lo que la función de onda asociada (ec. (14)) no
será físicamente aceptable. Entonces, la única manera de
que la condición (20) se cumpla para todo valor de
, por lo que la función de onda asociada (ec. (14)) no
será físicamente aceptable. Entonces, la única manera de
que la condición (20) se cumpla para todo valor de ![]() en
en
![]() , es que los términos encerrados por los
corchetes en (18) y (19) sean polinomios; sean estos polinomios
, es que los términos encerrados por los
corchetes en (18) y (19) sean polinomios; sean estos polinomios
![]() y
y ![]() , definidos por:
, definidos por:
| (21) |
| (22) |
De (21) y (22):
| (23) |
Si ![]() es un polinomio,
es un polinomio, ![]() lo será también si y sólo si
lo será también si y sólo si
![]() y
y
![]() con
con
![]() números
enteros, los cuales pueden ser positivos o negativos, sujetos en
este último caso a la condición de que
números
enteros, los cuales pueden ser positivos o negativos, sujetos en
este último caso a la condición de que ![]() tenga como factor
un polinomio divisible entre
tenga como factor
un polinomio divisible entre
![]() en el anillo de polinomios.
en el anillo de polinomios.
Lo anterior implica, ya que
![]() y
y
![]() , que
, que ![]() y
y
![]() deben ser los dos enteros o los dos semienteros. Este es el mismo resultado
de Dirac.
deben ser los dos enteros o los dos semienteros. Este es el mismo resultado
de Dirac.
No se presenta el tratamiento anterior en las coordenadas cuadrático
parabólicas originales pues, haciendo un exámen del mismo, se
ve que su éxito está basado en que fue posible obtener
ecuaciones del tipo (15) para las ![]() 's, o sea, ecuaciones
diferenciales de una sola variable. Esto se debe a que las
coordenadas esféricas contienen una de longitud
's, o sea, ecuaciones
diferenciales de una sola variable. Esto se debe a que las
coordenadas esféricas contienen una de longitud ![]() y dos
de ángulo, teniendo que las eigenfunciones de
y dos
de ángulo, teniendo que las eigenfunciones de
![]() tienen las dependencias en
tienen las dependencias en ![]() y en
y en ![]() completamente diferenciadas, lo cual permite, tomando ventaja de
la sencilla dependencia en
completamente diferenciadas, lo cual permite, tomando ventaja de
la sencilla dependencia en ![]() (ec. (14)), obtener una
ecuación diferencial ordinaria para
(ec. (14)), obtener una
ecuación diferencial ordinaria para ![]() . Sin embargo, al usar
las coordenadas
. Sin embargo, al usar
las coordenadas
![]() , se obtiene que
, se obtiene que
![]() contienen derivadas con respecto a
contienen derivadas con respecto a
![]() . La derivada con respecto a
. La derivada con respecto a ![]() no causa
ningún problema (desaparece) por la misma razón considerada en
coordenadas esféricas, pero las derivadas con respecto a
no causa
ningún problema (desaparece) por la misma razón considerada en
coordenadas esféricas, pero las derivadas con respecto a ![]() y
y
![]() aparecen en forma más o menos simétrica, por lo que se
obtienen para las
aparecen en forma más o menos simétrica, por lo que se
obtienen para las ![]() 's ecuaciones diferenciales parciales con 2
variables.
's ecuaciones diferenciales parciales con 2
variables.
ii) Procedimento de Hurst. Realmente, el método de Fierz se ha
incluído por dos razones principales: para aclarar las
características básicas del procedimiento de Hurst y para
obtener un tipo de cuantización que es fundamentalmente distinto
del que se obtendrá ahora para
![]() usando el potencial
usando el potencial ![]() . Usando el ``potencial vectorial"
. Usando el ``potencial vectorial"
![]() (ec. (5)), se obtiene el resultado de que
(ec. (5)), se obtiene el resultado de que
![]() puede tomar valores
enteros y semienteros; al usar el potencial
puede tomar valores
enteros y semienteros; al usar el potencial ![]() (ec.
(2-a), sección I.C), se obtiene, como se verá a continuación,
que
(ec.
(2-a), sección I.C), se obtiene, como se verá a continuación,
que
![]() sólo puede tomar
valores enteros. Ya que
sólo puede tomar
valores enteros. Ya que ![]() y
y
![]() difieren
tan sólo en una norma (gauge) (ec. (21), Introducción), éste
es un resultado realmente inesperado. Se volverá sobre este punto
en la sección de conclusiones.
difieren
tan sólo en una norma (gauge) (ec. (21), Introducción), éste
es un resultado realmente inesperado. Se volverá sobre este punto
en la sección de conclusiones.
En lugar de considerar las ecuaciones para los operadores de escalera
(ecs. (18), (19)) se trabaja con la ecuación de eigenvalores para
el operador
![]() con
con
![]() dado
por la ec. (6). Ya que
dado
por la ec. (6). Ya que
![]() es una constante
del movimiento, lo es también
es una constante
del movimiento, lo es también
![]() , por lo
que sus eigenfunciones se pueden escoger como funciones, de onda.
Escribiendo estas funciones de onda en la forma:
, por lo
que sus eigenfunciones se pueden escoger como funciones, de onda.
Escribiendo estas funciones de onda en la forma:
| (24) |
![\begin{displaymath}
\overline{{\mathcal{D}}}^2 =-\hbar^2
\left[\frac{1}{\mbox{...
...\large$\varepsilon$}}}^2}{\hbar^2 \mbox{sen}^2\theta}\right]
\end{displaymath}](img1119.png) |
(25) |
| (26) |
Escribiendo ahora:
| (27) |
| (28) |
Sea:
| (29) |
Escribiendo:
| (30) |
| (31) |
| (32) |
| (33) |
| (34) |
Usando las ecs. (33,34) en (32) resulta la siguiente ecuación
diferencial para ![]() :
:
| (35) |
Pero la ecuación (35) es idéntica a la ecuación hipergeométrica [70]:
| (36) |
| (37) |
| (38) |
| (39) |
La solución de (36) se escribe en la forma [70]:
| (40) |
Usando las ecs. (37-39, 34) se obtiene para ![]() :
:
| (41) |
De acuerdo con las ecuaciones (25,26), la función ![]() debe ser
regular (debe existir su derivada - la cual debe ser derivable
también, según (25)-) en todo su dominio de definición. En
coordenadas esféricas,
debe ser
regular (debe existir su derivada - la cual debe ser derivable
también, según (25)-) en todo su dominio de definición. En
coordenadas esféricas, ![]() se define entre 0 y
se define entre 0 y ![]() .
Entonces, usando las ecuaciones (33,29) se tiene que el intervalo de
definición de
.
Entonces, usando las ecuaciones (33,29) se tiene que el intervalo de
definición de ![]() es [0,1]. Entonces, la función
es [0,1]. Entonces, la función ![]() debe ser regular en el intervalo [0,1]; en particular, la
regularidad de
debe ser regular en el intervalo [0,1]; en particular, la
regularidad de ![]() en 0 y en 1 implica, como se verá en lo
siguiente, la cuantización de
en 0 y en 1 implica, como se verá en lo
siguiente, la cuantización de ![]() y
y ![]() .
.
En el análisis que sigue, sea ![]() ; como se verá al final
del mismo, este requerimiento no implica ninguna restricción
sobre la validez general del estudio y se hace sólo por razones
de concretez en los argumentos. Hay que considerar los siguientes
casos:
; como se verá al final
del mismo, este requerimiento no implica ninguna restricción
sobre la validez general del estudio y se hace sólo por razones
de concretez en los argumentos. Hay que considerar los siguientes
casos:
i) Para ![]() , la regularidad de
, la regularidad de ![]() implica
implica ![]() .
.
ii) Para ![]() , usando la fórmula (71) para desarrollar la función
hipergeométrica con respecto al punto
, usando la fórmula (71) para desarrollar la función
hipergeométrica con respecto al punto ![]() :
:
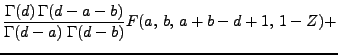 |
(42) | ||
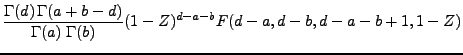 |
(43) |
se obtiene regularidad de ![]() en
en ![]() si y
sólo si
si y
sólo si ![]() , con
, con ![]() un entero positivo ó 0 (en cuyo caso
la serie que se tiene en (41) se reduce a un polinomio); o sea, si
y sólo si (usando la ec. (37)):
un entero positivo ó 0 (en cuyo caso
la serie que se tiene en (41) se reduce a un polinomio); o sea, si
y sólo si (usando la ec. (37)):
| (44) |
La razón de lo anterior es la siguiente: al usar la fórmula (42))
aparece en el 2do. término del lado derecho de la misma una potencia de
![]() de la forma:
de la forma:
![]() , lo
cual implica que la potencia de
, lo
cual implica que la potencia de ![]() que aparece en la ec. (41)
es
que aparece en la ec. (41)
es
![]() . Entonces, la condición
. Entonces, la condición ![]() implica
implica
![]() , lo cual implica que hay
regularidad de
, lo cual implica que hay
regularidad de ![]() en
en ![]() si y sólo si el segundo
término del lado derecho, de la ec. (42) es 0; ésto es posible
si y sólo si
si y sólo si el segundo
término del lado derecho, de la ec. (42) es 0; ésto es posible
si y sólo si ![]() ó
ó ![]() (o ambas) son enteros negativos ó 0,
pues
(o ambas) son enteros negativos ó 0,
pues ![]() y
y ![]() aparecen en el denominador del
término que se quiere anular; la condición sobre
aparecen en el denominador del
término que se quiere anular; la condición sobre ![]() ó
ó ![]() es
necesaria y suficiente pues la función
es
necesaria y suficiente pues la función ![]() , para argumento
real, nunca [72] es 0, por lo que, para anular términos de
la forma
, para argumento
real, nunca [72] es 0, por lo que, para anular términos de
la forma
![]() como el que aparece en la
expresión que se desea anular, la única manera de hacerlo es
haciendo
como el que aparece en la
expresión que se desea anular, la única manera de hacerlo es
haciendo ![]() un entero negativo ó 0, pues sólo en estos
casos [72]
un entero negativo ó 0, pues sólo en estos
casos [72]
![]() .
.
i) Para ![]() , hay regularidad de
, hay regularidad de ![]() si
si ![]()
ii) Para ![]() , usando nuevamente la expresión (42),
se obtiene regularidad de
, usando nuevamente la expresión (42),
se obtiene regularidad de ![]() si
si ![]() , con
, con ![]() un entero positivo ó 0; sea, si:
un entero positivo ó 0; sea, si:
| (45) |
La razon es la siguiente: la potencia de ![]() que aparece en (42)
es
que aparece en (42)
es
![]() , lo cual implica que, en (41), la
potencia de
, lo cual implica que, en (41), la
potencia de ![]() que es factor del primer término de (42) es
que es factor del primer término de (42) es
![]() y la que es factor de 2o.
término de (42) es
y la que es factor de 2o.
término de (42) es
![]() ; con la
segunda de estas potencias no hay problema de regularidad en
; con la
segunda de estas potencias no hay problema de regularidad en ![]() , pues
, pues
![]() sin embargo, ya que
sin embargo, ya que
![]() , se
obtiene regularidad de
, se
obtiene regularidad de ![]() si y sólo si el primer término
en la ec. (42) se anula, si y sólo si
si y sólo si el primer término
en la ec. (42) se anula, si y sólo si ![]() ó
ó ![]() son
enteros negativos ó 0.
son
enteros negativos ó 0.
i) Para ![]() , la regularidad de
, la regularidad de ![]() implica
implica ![]() .
.
ii) Para ![]() , hay regularidad de
, hay regularidad de ![]() si:
si:
| (46) |
El resultado (45) se obtiene de considerar la ec. (42) para el segundo
sumando del lado derecho en (41); al hacerlo, se obtiene que, en
(41), la potencia de ![]() que es factor del primer sumando en
(42) es
que es factor del primer sumando en
(42) es
![]() y la que es factor del
segundo sumando es
y la que es factor del
segundo sumando es
![]() ; con esta
segunda potencia no hay problema de regularidad en
; con esta
segunda potencia no hay problema de regularidad en ![]() , pues
, pues
![]() ; sin embargo, ya que
; sin embargo, ya que
![]() , para obtener
regularidad de
, para obtener
regularidad de ![]() , se debe tener que el 1er. sumando que
resulta de la aplicación de (42) sea 0, lo cual se logra si y
sólo si
, se debe tener que el 1er. sumando que
resulta de la aplicación de (42) sea 0, lo cual se logra si y
sólo si ![]() ó
ó
![]() (ó ambas) son enteros
negativos ó 0; trabajando con
(ó ambas) son enteros
negativos ó 0; trabajando con ![]() , se tiene que, si
, se tiene que, si ![]() es un entero positivo ó 0, la condición de regularidad de
es un entero positivo ó 0, la condición de regularidad de
![]() en
en ![]() es
es
![]() , de la cual se obtiene la
relación (45).
, de la cual se obtiene la
relación (45).
Usando las relaciones (43,44,45) se obtiene la siguiente gráfica de ![]() contra
contra ![]() :
:
Un exámen de la gráfica anterior indica que las
funciones
![]() dan una base de
representación del grupo 0(3) si y sólo si:
dan una base de
representación del grupo 0(3) si y sólo si:
| (47) |
De la fig. 1, es claro que el único efecto de cambiar el valor de
![]() consiste en un cambio en el nivel de la línea
marcada
consiste en un cambio en el nivel de la línea
marcada ![]() . Cuando se toman valores negativos de
. Cuando se toman valores negativos de ![]() ,
el único cambio que resulta es que (44) se convierte en
,
el único cambio que resulta es que (44) se convierte en
![]() y que en (46)
y que en (46) ![]() representa al entero mayor
que
representa al entero mayor
que ![]() más próximo a él. También es claro, de la
fig. 1 y de estas últimas consideraciones, que:
más próximo a él. También es claro, de la
fig. 1 y de estas últimas consideraciones, que:
| (48) |
El resultado anterior implica:
| (49) |
Las expresiones (47,48) indican que el momento angular total siempre
es mayor que
![]() . Este resultado ya fué
mencionado en la sección I.B, en relación con su análogo
clásico (ecs. (11,12, 12-a), sección I.B).
. Este resultado ya fué
mencionado en la sección I.B, en relación con su análogo
clásico (ecs. (11,12, 12-a), sección I.B).