Ya que se usarán las coordenadas cuadrático parabólicas,
es necesario poner el
Hamiltoniano en estas coordenadas. Hay más de una manera de
hacer esto. De acuerdo con una de ellas, hay que partir del
Hamiltoniano clásico (ec.(2), sección I.C) y siguiendo el
método de Schrödinger [49] obtener el Hamiltoniano
cuántico en coordenadas cartesianas, para usar después las
ecs. (3, 4, 5), sección I-C y la regla de la cadena con el
cambio a las coordenadas ![]() y
y ![]() , etc. De acuerdo con
otro de los métodos, se puede escribir directamente el
Hamiltoniano cuántico en las coordenadas que se usarán,
empleando el procedimiento de Podolsky [50] para pasar de la
descripción cuántica en unas coordenadas a la correspondiente
en otro sistema arbitrario. El procedimiento de cuantización
canónica [51] no puede usarse en este caso, pues las
coordenadas y momenta
, etc. De acuerdo con
otro de los métodos, se puede escribir directamente el
Hamiltoniano cuántico en las coordenadas que se usarán,
empleando el procedimiento de Podolsky [50] para pasar de la
descripción cuántica en unas coordenadas a la correspondiente
en otro sistema arbitrario. El procedimiento de cuantización
canónica [51] no puede usarse en este caso, pues las
coordenadas y momenta
![]() no están conectados con
los
no están conectados con
los
![]() por una transformación unitaria,
lo cual es claro del hecho de que no tienen los mismos rangos las
variables
por una transformación unitaria,
lo cual es claro del hecho de que no tienen los mismos rangos las
variables ![]() y
y
![]() (
(
![]() las primeras y
las primeras y ![]() y
y ![]() respectivamente, las
segundas).
respectivamente, las
segundas).
Se usó el primer método de los anotados anteriormente, pues la
aplicación del mismo resulta muy larga en el paso de coordenadas
cartesianas a cuadrático-parabólicas. El procedimiento de
Podolsky se basa en una forma de normalización de las funciones
de onda que es independiente de Jacobianos, y en el uso de una
expresión para el Hamiltoniano en las nuevas coordenadas la cual
no es trivial, pues contiene términos del tipo ![]() , los
cuales denotan los menores del tensor métrico; debido a la
longitud de las expresiones algebraicas resultantes, no se
empleó este método.
, los
cuales denotan los menores del tensor métrico; debido a la
longitud de las expresiones algebraicas resultantes, no se
empleó este método.
La ecuación de Schrödinger independiente del tiempo es:
| (1) |
El Hamiltoniano clásico es: (ec. (2), sección I.C):
| (2) |
Siguiendo el procedimiento de cuantización de Schrödinger [45] y usando la ec. (2-a) de la sección I.C, se puede escribir:
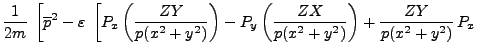 |
|||
![$\displaystyle \left. \left. - \frac{ZX}{p(x^2+y^2)} P_y\right]
+ \frac {\varep...
...] +
\frac{e_1 e_2}{p} + \frac{\varepsilon^2}{2m} \left( \frac{1}
{p^2} \right)$](img885.png) |
(3) |
Trabajando en la representación de coordenadas [52] ( en la cual hay que
hacer las substituciones
![]() ), se
obtiene:
), se
obtiene:
| (4) |
Se pasará ahora a las coordenadas
![]() .
Usando las ecs. (3,4,5) de la sección I.C se puede
escribir [53].
.
Usando las ecs. (3,4,5) de la sección I.C se puede
escribir [53].
![$\displaystyle \nabla^2 = \frac 1 { \mu^2+ \nu^2 } \left [ \frac {\partial^2} {\...
... \partial {\partial \mu} + \frac 1 { \nu} \frac \partial {\partial \nu} \right]$](img889.png) |
(5) |
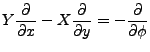 |
(6) |
De las ecs. (4,5,6) se obtiene:
![$\displaystyle \frac 1 {2m ( \mu^2+ \nu^2)} \left \{ \left(-i \hbar \frac \parti...
... \hbar \frac \partial { \partial \phi}\right)- \varepsilon \right ]^2
\right. +$](img891.png) |
|||
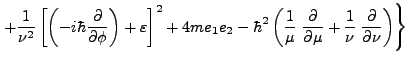 |
(7) |
Comparando la ec.(7) con la ec. (17) de la sección I.C, se vé que
excepto por el término
![]() , la expresión (7) se obtiene de
la (17) (sección I.C) haciendo las substituciones
, la expresión (7) se obtiene de
la (17) (sección I.C) haciendo las substituciones
![]() ; éstas son
las substituciones que indicaría el proceso de cuantización
canónica [47]. El último término de la ec. (7)
proviene de que, como se dijo anteriormente, las coordenadas
; éstas son
las substituciones que indicaría el proceso de cuantización
canónica [47]. El último término de la ec. (7)
proviene de que, como se dijo anteriormente, las coordenadas
![]() no se obtiene de las
no se obtiene de las
![]() por una transformación unitaria, por lo que el
proceso de cuantización canónica no es aplicable.
por una transformación unitaria, por lo que el
proceso de cuantización canónica no es aplicable.
De la ec. (7), se tiene que la coordenada ![]() es cíclica en
la ec. de Schrödinger, por lo cual [54] se tiene una solución del
tipo siguiente para la ec. (1):
es cíclica en
la ec. de Schrödinger, por lo cual [54] se tiene una solución del
tipo siguiente para la ec. (1):
| (8) |
Suponiendo que:
| (9) |
se obtiene, de las ecs. (1) y (7):
![$\displaystyle \left [ \frac 1 {F} \; \left( \frac{ d^2 F} {d \mu^2}
+ \frac 1 {...
...alpha ^2 - \frac {2m e_1 e_2}{\hbar^2} + \frac {2mE }{\hbar^2} \mu^2 \right ] +$](img898.png) |
|||
![$\displaystyle +\left [ \frac 1 {G} ( \frac {d^2 G }{d \nu^2} + \frac 1{\nu}\; \...
...\beta^2 - \frac {2m e_1 e_2}{\hbar^2} + \frac {2mE}{\hbar^2} \nu^2 \right ] = 0$](img899.png) |
(10) |
En la ec. (10):
| (11) | |||
| (12) |
Es claro de la ec. (10) que se ha obtenido la separación completa
de variables en la ecuación diferencial (1). Llamando ![]() a
la constante de separación y definiendo las cantidades (constantes):
a
la constante de separación y definiendo las cantidades (constantes):
| (13) | |||
| (14) | |||
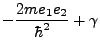 |
(15) | ||
| (16) | |||
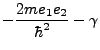 |
(17) |
Se obtienen las ecuaciones diferenciales que debe satisfacer ![]() y
y ![]() :
:
 |
(18) | ||
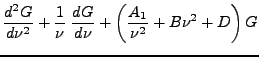 |
(19) |
Es claro, de las ecs. (18,19) que ![]() y
y ![]() satisfacen ecuaciones
diferenciales esencialmente idénticas. Basta, entonces, resolver
una de ellas para obtener la solución de las dos, pues la solución de la
otra ecuación se obtiene haciendo los cambios
satisfacen ecuaciones
diferenciales esencialmente idénticas. Basta, entonces, resolver
una de ellas para obtener la solución de las dos, pues la solución de la
otra ecuación se obtiene haciendo los cambios
![]() ,
,
![]() . Era de esperarse lo anterior de la simetría de la expresión (7) con respecto
a
. Era de esperarse lo anterior de la simetría de la expresión (7) con respecto
a ![]() y
y ![]() , y de las ecs. (3,4,5) de la sección I.C, en
las cuales
, y de las ecs. (3,4,5) de la sección I.C, en
las cuales ![]() y
y ![]() aparecen también simétricamente. Se
trabajará con la ecuación (18).
aparecen también simétricamente. Se
trabajará con la ecuación (18).
La ecuación (18) se puede resolver de dos maneras: directamente,
por series o transformándola para identificar una ecuación diferencial
conocida. Ya que el resultado esencial es obtener la cuantización
de
![]() y, debido a que dicha cuantización no
pudo obtenerse de las consideraciones comunes sobre la función de onda
( integrabilidad cuadrática y finitud de la densidad de corriente de
probabilidad), se incluirán los dos procedimientos, para apreciar más
claramente las dificultades.
y, debido a que dicha cuantización no
pudo obtenerse de las consideraciones comunes sobre la función de onda
( integrabilidad cuadrática y finitud de la densidad de corriente de
probabilidad), se incluirán los dos procedimientos, para apreciar más
claramente las dificultades.
a) Solución de la ec. (18) por series:
La ec. (18) no es soluble directamente por serie de potencias, pues
la relación de recursión obtenida para los coeficientes de la misma
involucra 3 índices, complicando su cálculo. Como es usual en esto
casos [55], se hallará primero el comportamiento asintótico de
la solución (cuando
![]() ). El procedimiento que
se sigue es matemáticamente incompleto, pues no se demuestra el hecho en
el cual se basa, el cual es el siguiente: el problema
de resolver una ecuación diferencial lineal ordinaria es realmente el
problema de hallar el Kernel de un operador lineal en un espacio de
funciones apropiado [56]; así, para ecuaciones de 2o. orden, el
Kernel es un espacio vectorial generado por combinaciones lineales de dos
funciones linealmente independientes (las soluciones independientes de la
ecuación); entonces, cuando se tiene que dos operadores diferenciales
). El procedimiento que
se sigue es matemáticamente incompleto, pues no se demuestra el hecho en
el cual se basa, el cual es el siguiente: el problema
de resolver una ecuación diferencial lineal ordinaria es realmente el
problema de hallar el Kernel de un operador lineal en un espacio de
funciones apropiado [56]; así, para ecuaciones de 2o. orden, el
Kernel es un espacio vectorial generado por combinaciones lineales de dos
funciones linealmente independientes (las soluciones independientes de la
ecuación); entonces, cuando se tiene que dos operadores diferenciales
![]() son tales que, al variar apropiadamente un parámetro
o la variable de la cual dependen las funciones del espacio sobre el cual
actúan
son tales que, al variar apropiadamente un parámetro
o la variable de la cual dependen las funciones del espacio sobre el cual
actúan ![]() y
y
![]() , se espera ( éste es el
hecho que no se demuestra, pues dicha demostración no es esencial en lo
que sigue) que, siendo
, se espera ( éste es el
hecho que no se demuestra, pues dicha demostración no es esencial en lo
que sigue) que, siendo ![]() y
y ![]() los Kernels de
los Kernels de ![]() y
y ![]() ,
cuando el parámetro o variable antes dicho se varía,
,
cuando el parámetro o variable antes dicho se varía,
![]() .
En otras palabras, se espera que las soluciones independientes de
.
En otras palabras, se espera que las soluciones independientes de
![]() y
y ![]() sean muy parecidas cuando
sean muy parecidas cuando ![]() y
y ![]() lo son. Las condiciones
para que ésto suceda no son tenidas en cuenta aquí, siguiendo el
pensamiento de que es un proceso que ha funcionado en otras ocasiones [55].
lo son. Las condiciones
para que ésto suceda no son tenidas en cuenta aquí, siguiendo el
pensamiento de que es un proceso que ha funcionado en otras ocasiones [55].
De acuerdo con lo anterior, de la ec. (18) se tiene que, cuando
![]() , para
, para
![]() acotada (lo cual es esencial para la
finitud de la densidad de corriente de probabilidad, que se define [57]
en términos del gradiente de la función de onda), se obtiene la ecuación
diferencial:
acotada (lo cual es esencial para la
finitud de la densidad de corriente de probabilidad, que se define [57]
en términos del gradiente de la función de onda), se obtiene la ecuación
diferencial:
| (20) |
En la ec. (20), ![]() denota la función a la cual tiende F
cuando
denota la función a la cual tiende F
cuando
![]() ; o sea,
; o sea, ![]() es tal que
es tal que
![]() .
.
Se comprueba por substitución en (20) que, siendo
![]() constantes:
constantes:
| (21) |
Se tiene, de la ec. (14), que:
Entonces, para
![]() ,
la función
,
la función ![]() dada por (21)
es oscilatoria: corresponde a una onda plana la función de onda
(pues se tiene lo mismo para la función G y para la
dependencia en
dada por (21)
es oscilatoria: corresponde a una onda plana la función de onda
(pues se tiene lo mismo para la función G y para la
dependencia en ![]() ), lo cuál era de esperarse, pues el
problema corresponde al movimiento de una partícula de masa
), lo cuál era de esperarse, pues el
problema corresponde al movimiento de una partícula de masa
![]() y carga eléctrica
y carga eléctrica ![]() que sufre Scattering por el
monopolo electromagnético, ya que, muy lejos de éste, la
partícula se mueve en forma libre ( no sujeta a potenciales ); en
este caso, se usa para normalizar a la función de onda alguno de
los métodos usuales [58] (normalización en una caja - ``box
normalization" etc. ). Para
que sufre Scattering por el
monopolo electromagnético, ya que, muy lejos de éste, la
partícula se mueve en forma libre ( no sujeta a potenciales ); en
este caso, se usa para normalizar a la función de onda alguno de
los métodos usuales [58] (normalización en una caja - ``box
normalization" etc. ). Para
![]() , lo que implica que
, lo que implica que
![]() da un comportamiento aceptable (se puede normalizar la
función de onda) sólo para
da un comportamiento aceptable (se puede normalizar la
función de onda) sólo para ![]() ; ya que en
el caso clásico se estudiarán los estados de moviento acotado
; ya que en
el caso clásico se estudiarán los estados de moviento acotado
![]() , se continuará la presente discusión con esta
hipótesis, o sea, se tomará como comportamiento asintótico
aceptable de F, la función:
, se continuará la presente discusión con esta
hipótesis, o sea, se tomará como comportamiento asintótico
aceptable de F, la función:
| (22) |
Se probará ahora [55] como solución de (18) a:
| (23) |
Con:
| (24) |
Por substitución de (23) en (18), se obtiene que la ecuación diferencial que
debe satisfacer ![]() es:
es:
| (25) |
Suponiendo posible para ![]() una expansión en serie de potencias:
una expansión en serie de potencias:
 |
(26) |
con [54]
![]() , se obtiene la ecuación,
indicial:
, se obtiene la ecuación,
indicial:
| (27) |
y la relación de recursión para los coeficientes ![]() :
:
| (28) |
De las ecs. (13,11) se tiene que
![]() , por lo que, de la ec. (27), se obtiene:
, por lo que, de la ec. (27), se obtiene:
| (29) |
La ec. (29) tiene las raíces:
| (30) | |||
| (31) |
Al considerar las potencias de ![]() que aparecen al substituir (26) en (25), se
tiene, para el coeficiente de
que aparecen al substituir (26) en (25), se
tiene, para el coeficiente de
![]() ,
pero, de (27), ésto implica que
,
pero, de (27), ésto implica que ![]() , lo cual implica, de
(28), que todos los coeficientes de índice impar son
, lo cual implica, de
(28), que todos los coeficientes de índice impar son ![]() .
.
Entonces, la solución general de (25) se puede escribir en la forma [59]:
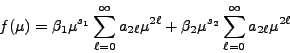 |
(32) |
con
![]() constantes.
constantes.
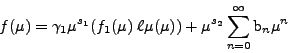 |
(33) |
Con ![]() una constante. Los coeficientes
una constante. Los coeficientes ![]() que aparecen en (33)
son hallados [59] substituyendo (33) en (25).
que aparecen en (33)
son hallados [59] substituyendo (33) en (25).
De hecho, como se demostrará más adelante,
![]() es siempre un entero, por lo que la solución adecuada a (25)
será de la forma (33).
es siempre un entero, por lo que la solución adecuada a (25)
será de la forma (33).
Se estudiará ahora el comportamiento de la función
![]() ; de
dicho estudio y de uno similar para la solución correspondiente
de la ec. (19), se obtendrá una fórmula para le energía.
; de
dicho estudio y de uno similar para la solución correspondiente
de la ec. (19), se obtendrá una fórmula para le energía.
De la ec. (28), se tiene que, para ![]() grande:
grande:
| (34) |
Pero, del estudio de la serie de potencias para
![]() :
:
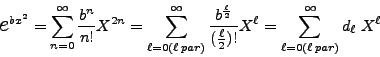 |
(35) |
se tiene que, para ![]() grande:
grande:
| (36) |
De las expresiones (34,36), se tiene que ![]() se comporta,
esencialmente, como la función
se comporta,
esencialmente, como la función
![]() ; pero, de la ec. (23), se tiene que
; pero, de la ec. (23), se tiene que ![]() se comporta,
en este caso, como la función
se comporta,
en este caso, como la función
![]() . Ya que (ec. (24))
. Ya que (ec. (24)) ![]() , éste no es un
comportamiento aceptable para
, éste no es un
comportamiento aceptable para ![]() , si se quiere
integrabilidad cuadrática de la función de onda. Entonces,
para obtener un comportamiento de
, si se quiere
integrabilidad cuadrática de la función de onda. Entonces,
para obtener un comportamiento de ![]() tal que se pueda tener
integrabilidad cuadrática, es necesario cortar la serie para
tal que se pueda tener
integrabilidad cuadrática, es necesario cortar la serie para
![]() o sea, obtener polinomios de ella, para cada valor de
o sea, obtener polinomios de ella, para cada valor de
![]() . Lo anterior es posible si y sólo si para un valor dado
. Lo anterior es posible si y sólo si para un valor dado
![]() de
de
![]() (en este caso, se obtiene un polinomio
de grado
(en este caso, se obtiene un polinomio
de grado ![]() ), ésto es posible si y sólo si (ec. (28)):
), ésto es posible si y sólo si (ec. (28)):
| (37) |
Haciendo para la ec. (19) el mismo análisis que para (28), se
encuentra, si ![]() toma el papel que tenía
toma el papel que tenía ![]() para la ec.
(25), que las ecuaciones correspondientes a (29,30,31,37) son:
para la ec.
(25), que las ecuaciones correspondientes a (29,30,31,37) son:
 |
(38) |
| (39) |
| (40) |
| (41) |
De las ecs. (37,44,15,17,24), se obtiene la siguiente fórmula para la energía:
| (42) |
Ya que ![]() y
y ![]() pueden tomar cualquier valor entero par no-negativo, se
tiene de la fórmula (42) que la energía toma valores
negativos de módulo arbitrariamente grande cuando
pueden tomar cualquier valor entero par no-negativo, se
tiene de la fórmula (42) que la energía toma valores
negativos de módulo arbitrariamente grande cuando ![]() es
próximo a un entero negativo de módulo mayor o igual que 2.
Esto sugiere que la suma
es
próximo a un entero negativo de módulo mayor o igual que 2.
Esto sugiere que la suma ![]() debe estar cuantizada de tal
manera que lo anterior no suceda. Esta última cuantización no
es implicada por (42), pues puede evitarse ese resultado
físicamente absurdo si
debe estar cuantizada de tal
manera que lo anterior no suceda. Esta última cuantización no
es implicada por (42), pues puede evitarse ese resultado
físicamente absurdo si ![]() es un número tal que
es un número tal que
![]() , siendo
, siendo ![]() un entero
positivo y
un entero
positivo y ![]() , sin embargo, esta condición no es nada
conclusiva sobre
, sin embargo, esta condición no es nada
conclusiva sobre ![]() y es muy artificial. De las ecs. (30, 31,
34, 40), se tiene que
y es muy artificial. De las ecs. (30, 31,
34, 40), se tiene que ![]() puede tomar los valores
puede tomar los valores
![]() ; entonces, la ec. (42) sugiere la
cuantización de
; entonces, la ec. (42) sugiere la
cuantización de ![]() y
y
![]() .
.
Si
Esta condición es equivalente a uno de los requerimientos para que
las funciones de onda formen un espacio de Hilbert: convierte a su
conjunto en un espacio métrico (el otro requerimiento se refiere
a la completez de este espacio métrico). Tomando, por ejemplo,
la función ![]() dada por (32) (la serie que allí
aparece, según se vió, debe ser cortada en un polinomio) y,
para la variable
dada por (32) (la serie que allí
aparece, según se vió, debe ser cortada en un polinomio) y,
para la variable ![]() , una solución semejante, se tiene, ya
que al jacobiano en las coordenadas
, una solución semejante, se tiene, ya
que al jacobiano en las coordenadas
![]() es [61]
es [61]
![]() que hay integrabilidad
cuadrática para
que hay integrabilidad
cuadrática para ![]() .
.
Tomando la función ![]() dada por (32) de tal manera que al
polinomio que aparece en el lugar de la serie se le llama
dada por (32) de tal manera que al
polinomio que aparece en el lugar de la serie se le llama ![]() y considerando
y considerando ![]() por simplicidad (para
por simplicidad (para
![]() se obtiene el mismo resultado y se alargan las
expresiones) y haciendo algo similar para la variable
se obtiene el mismo resultado y se alargan las
expresiones) y haciendo algo similar para la variable ![]() en
cuyo caso se toma un polinomio
en
cuyo caso se toma un polinomio ![]() en el papel de
en el papel de ![]() , se tiene que:
, se tiene que:
Ya que la densidad de corriente de probabilidad se define como [57]
siendo ![]() la función de onda y por la expresión del
gradiente [62] en las coordenadas
la función de onda y por la expresión del
gradiente [62] en las coordenadas
![]() :
:
| (43) |
Y tomando en cuenta que (con
![]() ):
):
 |
(44) | ||
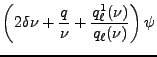 |
(45) | ||
| (46) |
Se comprueba que, cuando ![]() , hay finitud de
, hay finitud de ![]() para
para ![]() ;
cuando
;
cuando ![]() , hay finitud de
, hay finitud de ![]() para
para ![]() .
.
Se ve entonces que, como se dijo anteriormente, la directa aplicación de las
condiciones de integrabilidad cuadrática de la función de onda
y de finitud de ![]() no implican la cuantización de
no implican la cuantización de
![]() , que es un resultado al cual se quiere
llegar en forma esencial. En lugar de usar las expresiones para
, que es un resultado al cual se quiere
llegar en forma esencial. En lugar de usar las expresiones para
![]() (y las correspondientes para
(y las correspondientes para ![]() ) que se
usaron, se pudo haber trabajado con las funciones del tipo (33),
pero no se tiene ninguna razón aparente para rechazar a las que
se usaron, pues dicho rechazo es a posteriori: después de
demostrar la cuantización de
) que se
usaron, se pudo haber trabajado con las funciones del tipo (33),
pero no se tiene ninguna razón aparente para rechazar a las que
se usaron, pues dicho rechazo es a posteriori: después de
demostrar la cuantización de ![]() y
y
![]() .
.
b) Solución de la ec. (18) por identificación con la
ecuación confluente hipergeométrica.
Como se vió anteriormente, si se supone que
![]() satisface la ecuación (25). Suponiendo ahora que:
satisface la ecuación (25). Suponiendo ahora que:
| (47) |
con ![]() dada por la ec. (27), se obtiene, substituyendo en (25), que
dada por la ec. (27), se obtiene, substituyendo en (25), que ![]() debe satisfacer la ecuación;
debe satisfacer la ecuación;
| (48) |
Haciendo ahora el cambio de variable;
| (49) |
se obtiene (![]() está dada por la ec. (24)) la ecuación:
está dada por la ec. (24)) la ecuación:
| (50) |
La ec. (50) es idéntica a la ecuación confluente hipergeométrica [65].
| (51) |
Haciendo las indentificaciones:
| (52) | |||
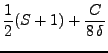 |
(53) |
Entonces [63], la función ![]() se puede escribir en la forma general:
se puede escribir en la forma general:
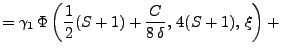 |
|||
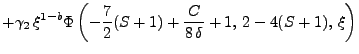 |
(54) |
con
![]() constantes y:
constantes y:
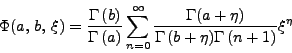 |
(55) |
Entonces, de las ecs. (49,47,23), se obtiene;
| (56) |
Del estudio del comportamiento de
![]() se encuentra [64] que sólo se puede cuantizar en el caso en que la serie (55) se reduce a un polinomio, lo cual sucede, siendo
se encuentra [64] que sólo se puede cuantizar en el caso en que la serie (55) se reduce a un polinomio, lo cual sucede, siendo ![]() enteros positivos, para:
enteros positivos, para:
| (57) |
| (58) |
De las ecs. (53, 58) se obtiene:
| (59) |
Se puede hacer un análisis análogo al anterior para la ec. (19), en
cuyo caso, según se dijo anteriormente, sólo hay que hacer los cambios
![]() : la ecuación análoga a (59) resultante es:
: la ecuación análoga a (59) resultante es:
| (60) |
Con ![]() dado por la ec. (38) y
dado por la ec. (38) y ![]() entero positivo. Usando las ecs.
(59,60) y las definiciones (24,15,17) y llamando
entero positivo. Usando las ecs.
(59,60) y las definiciones (24,15,17) y llamando
![]() , se
obtiene una fórmula para la energía:
, se
obtiene una fórmula para la energía:
| (61) |
Esta fórmula es idéntica a la obtenida anteriormente al resolver
las ecs. (18,19) por series (lo cual es un resultado obligatorio). Sin
embargo, ésto indica que de las condiciones comunes sobre el comportamiento
de la función obtenida, no se obtienen resultados más completos que los
que da el primer método de solución. En conclusión, la cuantización de
![]() y
y
![]() no puede obtenerse de propiedades directas de la función confluente hipergeométrica.
no puede obtenerse de propiedades directas de la función confluente hipergeométrica.
Como se ve, entonces, hay que utilizar otros métodos para obtener el resultado de cuantización deseado.