Como es sabido, dado un sistema físico descrito por cierto número de variables (observables), la estructura algebraica de éstas se basa, clásicamente, en sus relaciones de paréntesis de Poisson y, cuánticamente, en sus relaciones de conmutación.
Entonces, clásicamente, uno de los métodos de estudio de las simetrías de un sistema se basa en las estructuras algebraicas que se pueden formar a partir de funciones de las coordenadas y momenta que constituyen el espacio fase que le corresponde; otro método de estudio consiste en la identificación de las constantes del movimiento con significado geométrico más o menos directo, usando muchas veces para ésto, procedimientos vectoriales (en este trabajo se han usado los dos métodos, en las secciones I.C y I.B, respectivamente). Así, cuando se quiere estudiar la simetría de un sistema basándose en el primer método (``algebraico''), se buscan funciones de las coordenadas y momenta, independientes explícitamente del tiempo, que:
El concepto de grupo dinámico puede considerarse ya como un poco antigüo [36],
siendo motivado por ciertas observaciones y el deseo de algunas
personas [36,37], de dar un tratamiento basado puramente
en teoría de Grupos a ciertos problemas, principalmente los
más extensamente estudiados: el de Kepler y el del oscilador
armónico [37,38,39], aunque también existe la idea
de dar un tratamiento similar a todos los problemas
dinámicos [36,37,38,45]. La idea surgió después
del famoso trabajo de Fock [40] de 1935, en el cual
demostró que el grupo de simetría para el problema de
Coulomb (átomo de Hidrógeno) es ![]() (aunque ésto estaba
implícito en el tratamiento de Pauli [41] del mismo
problema, de 1926). Las observaciones a que se hizo mención
anteriormente son en el sentido de que ciertos conjuntos de
eigen-funciones del Hamiltoniano de un problema cuántico, no
correspondiendo necesariamente al mismo eigenvalor, forman base de
representaciones de grupos. La referencia más antigua
conteniendo una formalización de estas ideas es un
artículo de Dothan, Gell-Mann y Neéman [43], en el
cual tratan de aplicarlas a la clasificación de partículas
elementales.
(aunque ésto estaba
implícito en el tratamiento de Pauli [41] del mismo
problema, de 1926). Las observaciones a que se hizo mención
anteriormente son en el sentido de que ciertos conjuntos de
eigen-funciones del Hamiltoniano de un problema cuántico, no
correspondiendo necesariamente al mismo eigenvalor, forman base de
representaciones de grupos. La referencia más antigua
conteniendo una formalización de estas ideas es un
artículo de Dothan, Gell-Mann y Neéman [43], en el
cual tratan de aplicarlas a la clasificación de partículas
elementales.
En el caso clásico, estas ideas forman la siguiente forma: dado un
problema descrito por un Hamiltoniano ![]() , se trata de
encontrar funciones independientes
, se trata de
encontrar funciones independientes ![]() tales que formen un
conjunto cerrado con respecto a la operación de paréntesis de
Poisson; las funciones
tales que formen un
conjunto cerrado con respecto a la operación de paréntesis de
Poisson; las funciones ![]() deben ser, en número, por lo menos
iguales a la dimensionalidad del espacio fase, para que sea
posible expresar a todas las variables y momenta
deben ser, en número, por lo menos
iguales a la dimensionalidad del espacio fase, para que sea
posible expresar a todas las variables y momenta ![]() en
función de ellas [44]. Partiendo de las funciones
en
función de ellas [44]. Partiendo de las funciones ![]() , se
forma un conjunto canónico [33] y se pone el Hamiltoniano
en función de las mismas. Las funciones
, se
forma un conjunto canónico [33] y se pone el Hamiltoniano
en función de las mismas. Las funciones ![]() constituyen los
generadores de un grupo de Lie al cual se le llama grupo de no
invariancia o grupo dinámico del problema; debido a su
estructura algebraica, dan la información sobre
características del sistema (energía, rangos de las
variables
constituyen los
generadores de un grupo de Lie al cual se le llama grupo de no
invariancia o grupo dinámico del problema; debido a su
estructura algebraica, dan la información sobre
características del sistema (energía, rangos de las
variables ![]() , etc.) de una manera más o menos
directa [36,45]. Esto equivale a un tratamiento del
problema con base sólo en teoría de Grupos. En cuanto al
número de funciones
, etc.) de una manera más o menos
directa [36,45]. Esto equivale a un tratamiento del
problema con base sólo en teoría de Grupos. En cuanto al
número de funciones ![]() , si éste excede a la dimensionalidad
del espacio fase, son de esperarse condiciones de restricción
entre ellas, por lo cual es apropiado cambiar del uso de
paréntesis de Poisson, a paréntesis de Dirac [36,38].
Generalmente se requiere, también, del grupo dinámico, que
contenga al de simetría. El primer trabajo en el cual se
aplica lo anterior al problema de Kepler es el de
Bacry [38], en el cual demuestra que el grupo de Desitter
, si éste excede a la dimensionalidad
del espacio fase, son de esperarse condiciones de restricción
entre ellas, por lo cual es apropiado cambiar del uso de
paréntesis de Poisson, a paréntesis de Dirac [36,38].
Generalmente se requiere, también, del grupo dinámico, que
contenga al de simetría. El primer trabajo en el cual se
aplica lo anterior al problema de Kepler es el de
Bacry [38], en el cual demuestra que el grupo de Desitter
![]() es de no invariancia para el problema.
Györgyi trató el mismo problema clásica [36] y
cuánticamente [38] y demostró que
es de no invariancia para el problema.
Györgyi trató el mismo problema clásica [36] y
cuánticamente [38] y demostró que ![]() es grupo de
no invariancia en ambos casos. Hwa y Nuyts [39] trataron el
problema del oscilador armónico y demostraron que
es grupo de
no invariancia en ambos casos. Hwa y Nuyts [39] trataron el
problema del oscilador armónico y demostraron que ![]() y
y
![]() son grupos de no invariancia para el oscilador
armónico isotrópico n-dimensional.
son grupos de no invariancia para el oscilador
armónico isotrópico n-dimensional.
Cuánticamente, debido al cambio fundamental en el método de descripción con respecto a la Mecánica Clásica, las ideas anteriores toman una forma un poco distinta:
La observación de que, dado un hamiltoniano con un cierto espectro de eigenvalores, había ciertos conjuntos de eigenfunciones que daban bases para representaciones de grupos, ha dado lugar a los conceptos: el de grupo de simetría y el de grupo dinámico o de no invariancia.
Un grupo de simetría de un sistema es un grupo cuyas representaciones
tienen como bases subconjuntos de ![]() con:
con:
La utilidad de conocer tales grupos es evidente cuando se tiene un
grupo ![]() tal que sus representaciones están dadas por
tal que sus representaciones están dadas por
![]() misma, para cada
misma, para cada ![]() . Entonces, una vez identificado este
grupo, se tiene información completa sobre la degeneración del
sistema, pues ella está dada por las dimensiones de las
representaciones de
. Entonces, una vez identificado este
grupo, se tiene información completa sobre la degeneración del
sistema, pues ella está dada por las dimensiones de las
representaciones de ![]() , siendo estas últimas conocidas.
Además, se tiene información sobre reglas de selección en
transiciones del sistema y sobre el cálculo de elementos de
matriz de operadores [46].
, siendo estas últimas conocidas.
Además, se tiene información sobre reglas de selección en
transiciones del sistema y sobre el cálculo de elementos de
matriz de operadores [46].
El concepto de grupo dinámico se originó en la observación [37,42]
de que ciertos subconjuntos de ![]() , siendo
, siendo ![]() el conjunto de eigenfunciones del Hamiltoniano, no correspondiendo
necesariamente a un sólo eigenvalor, dan representaciones de
grupos de transformaciones del Hamiltoniano. Entonces, si fuera
posible hallar un grupo tal que
el conjunto de eigenfunciones del Hamiltoniano, no correspondiendo
necesariamente a un sólo eigenvalor, dan representaciones de
grupos de transformaciones del Hamiltoniano. Entonces, si fuera
posible hallar un grupo tal que ![]() diera una base de
representación para él, se tendría completamente resuelto
el problema, pues se tendría, además de la degeneración,
dada por el grupo de simetría, el espectro de eigenvalores,
pues éste sería obtenido a partir de relaciones de los
generadores del grupo.
diera una base de
representación para él, se tendría completamente resuelto
el problema, pues se tendría, además de la degeneración,
dada por el grupo de simetría, el espectro de eigenvalores,
pues éste sería obtenido a partir de relaciones de los
generadores del grupo.
El problema de Kepler y el oscilador armónico han sido tratados desde este punto de vista [36,37,38,39]. En general, el grupo dinámico no es único, teniéndose, cuando hay dos o más, que generan distintas porciones del espectro de eigenvalores [37].
Las ideas anteriores se han aplicado también de manera inversa: dado un grupo de Lie, se trata de construir, a partir de funciones de sus generadores, Hamiltonianos que tengan a dicho grupo como de no invariancia [45a]; para que dichos Hamiltonianos correspondan a los de sistemas físicos, se les requieren condiciones adicionales de Hermiticidad, invariancia respecto a inversión el tiempo, etc. [45a].
Para el problema que se ha estado tratando, se tiene, de las relaciones
(97,98) de la sec. I.C, que cualquier eigenfunción de
![]() en el conjunto (97) multiplicada por cualquiera
de las que están en (98), da una eigenfunción de
en el conjunto (97) multiplicada por cualquiera
de las que están en (98), da una eigenfunción de
![]() con eigenvalor 0, bajo paréntesis de Poisson; o
sea, estos productos dan funciones que generan transformaciones
canónicas que ``conservan" la carga magnética. Entre los 16
productos posibles, hay 8 que fueron ya utilizados en la
construcción del grupo de simetría del problema; los 8
productos restantes, sin embargo, son eigenfunciones del
Hamiltoniano (bajo paréntesis de Poisson) con eigenvalores
distintos de 0. Entonces, si se puede demostrar que los 16
productos de eigenfunciones de
con eigenvalor 0, bajo paréntesis de Poisson; o
sea, estos productos dan funciones que generan transformaciones
canónicas que ``conservan" la carga magnética. Entre los 16
productos posibles, hay 8 que fueron ya utilizados en la
construcción del grupo de simetría del problema; los 8
productos restantes, sin embargo, son eigenfunciones del
Hamiltoniano (bajo paréntesis de Poisson) con eigenvalores
distintos de 0. Entonces, si se puede demostrar que los 16
productos de eigenfunciones de ![]() son
generadores de un álgebra de Lie, se habrá demostrado la
existencia de un grupo dinámico para el problema, pues el
Hamiltoniano, según es evidente de la ec. (88) de la sección
I.C, se puede poner en función de ellas, lo mismo que todas las
variables y momenta canónicos
son
generadores de un álgebra de Lie, se habrá demostrado la
existencia de un grupo dinámico para el problema, pues el
Hamiltoniano, según es evidente de la ec. (88) de la sección
I.C, se puede poner en función de ellas, lo mismo que todas las
variables y momenta canónicos
![]() (en principio, para hacer ésto, se pueden
invertir las relaciones (125-128)
de la sección I.C ).
(en principio, para hacer ésto, se pueden
invertir las relaciones (125-128)
de la sección I.C ).
Fué posible demostrar que los 16 productos referidos son los generadores
del álgebra de Lie correspondiente al grupo ![]() ,
utilizando el procedimiento siguiente:
,
utilizando el procedimiento siguiente:
Sean
![]() los siguientes productos de funciones (97,98) de
la sección I.C (los 8 restantes ya fueron calculados, con los
nombres
los siguientes productos de funciones (97,98) de
la sección I.C (los 8 restantes ya fueron calculados, con los
nombres
![]() , ecs. (101-108), sec. I.C):
, ecs. (101-108), sec. I.C):
| (1) | |||
| (2) | |||
| (3) | |||
| (4) | |||
| (5) | |||
| (6) | |||
| (7) | |||
| (8) |
Ahora, se necesitan los paréntesis de Poisson de las B's con el
Hamiltoniano. Sin embargo, de la fórmula (88) de la sección
I.C, usando el hecho (consecuencia de la regla de la cadena) de
que, siendo ![]() ,
, ![]() y
y ![]() funciones de las variables canónicas
funciones de las variables canónicas
![]() ,
, ![]() :
:
![]() , se demuestra que; siendo
, se demuestra que; siendo ![]() una
función arbitraria de las
una
función arbitraria de las ![]() ,
, ![]() :
:
![\begin{displaymath}[H,f]= \left(\frac 2 {m e_1^2 e_2^2} \right)^{\frac 1 2}
(-E...
... 3 2}[a_1^+a_1^- + a_2^+a_2^- + a_3^+a_3^- + a_4^+a_4^-
, f]
\end{displaymath}](img701.png) |
(9) |
Pero, ya que el sistema es conservativo, ![]() cte., y el factor que
aparece enfrente del paréntesis de Poisson del lado derecho de
(9) puede hacerse igual a la unidad, escogiendo unidades
apropiadas. En este caso, puede aplicarse la fórmula:
cte., y el factor que
aparece enfrente del paréntesis de Poisson del lado derecho de
(9) puede hacerse igual a la unidad, escogiendo unidades
apropiadas. En este caso, puede aplicarse la fórmula:
| (10) |
Con:
| (11) |
Utilizando (11) y la ec. (91) de la sección I.C, se obtiene:
| (12) |
| (13) |
Los paréntesis de Poisson de las ![]() s y
s y ![]() s se dan en la tabla 1.
s se dan en la tabla 1.
0pt
| [f,g] | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 | |
|
0 | 0 | 0 | 0 | 0 | |
|
0 | 0 | |
0 | |
0 |
| |
0 |
|
|
0 | 0 | 0 | 0 | 0 | 0 | |
|
|
0 | |
0 | |
| |
|
0 | |
0 | 0 | 0 | 0 | |
|
0 | 0 | 0 | |
0 | |
|
| 0 | |
|
0 | 0 | 0 | 0 | 0 | 0 | 0 | |
|
0 | |
0 | |
|
| 0 | 0 | 0 | 0 | 0 | |
|
0 | |
0 | |
0 | |
|
0 | 0 | |
| 0 | 0 | 0 | 0 | |
0 |
|
|
|
0 | |
0 | 0 | 0 | |
|
|
| 0 | 0 | 0 | 0 | |
|
0 | |
0 | |
0 | |
|
|
0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | |
|
0 | 0 | |
0 | |
0 | 0 | |
|
|
| |
0 | |
0 | |
|
0 | 0 | 0 | 0 | 0 | 0 |
|
|
|
0 | |
| |
0 | |
0 | 0 | 0 | |
|
0 | 0 | 0 | 0 | |
0 |
|
|
|
| 0 | |
0 | |
|
|
0 | 0 | 0 | 0 | 0 | 0 | |
|
0 | |
|
| 0 | |
0 | |
0 | 0 | |
|
0 | 0 | 0 | 0 | 0 | |
|
|
|
| |
|
0 | 0 | |
0 | |
0 |
|
|
|
0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | |
|
|
0 | |
0 | |
0 |
|
|
0 | 0 | 0 | 0 | |
| |
|
0 | 0 | 0 | |
0 | |
|
|
0 | |
0 | 0 | 0 | 0 | |
| 0 | 0 | |
|
0 | |
0 | |
0 | |
|
|
0 | 0 | 0 | 0 |
Es claro, de la tabla 1, que el conjunto de las ![]() s y
s y ![]() s es cerrado
bajo la operación de paréntesis de Poisson; entonces,
constituye una álgebra de Lie [33]. Se trata ahora de
identificarla.
s es cerrado
bajo la operación de paréntesis de Poisson; entonces,
constituye una álgebra de Lie [33]. Se trata ahora de
identificarla.
Se hará la identificación del álgebra de Lie que se tiene por medio
de su diagrama de Schouten [47]. Este diagrama se construye
de la siguiente manera: se buscan los vectores
raíces [48] (root vectors) del álgebra de Lie que se
tiene; estos vectores raíces son elementos del espacio dual
de las ![]() s y
s y ![]() s para cuya identificación se usa la
subálgebra de Cartan del álgebra bajo estudio [33];
ésta es una subálgebra que es nilpotente y además, su propio
normalizador [33], estando constituida, salvo en casos
excepcionales, por el conjunto máximo de elementos del álgebra
que conmutan entre sí bajo paréntesis de Poisson. De entre
los vectores raíces, se seleccionan las raíces simples
(simple roots) [48] y de ellas se obtiene el diagrama de
Schouten buscado, por un procedimiento que se describirá en el
lugar apropiado.
s para cuya identificación se usa la
subálgebra de Cartan del álgebra bajo estudio [33];
ésta es una subálgebra que es nilpotente y además, su propio
normalizador [33], estando constituida, salvo en casos
excepcionales, por el conjunto máximo de elementos del álgebra
que conmutan entre sí bajo paréntesis de Poisson. De entre
los vectores raíces, se seleccionan las raíces simples
(simple roots) [48] y de ellas se obtiene el diagrama de
Schouten buscado, por un procedimiento que se describirá en el
lugar apropiado.
La subálgebra de Cartan del álgebra de Lie que se tiene está constituida por los siguientes elementos:
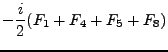 |
(14) | ||
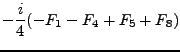 |
(15) | ||
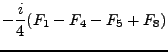 |
(16) | ||
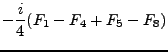 |
(17) |
En la identificación de las sumas de los lados derechos de (15-17) se usaron las ecs. (164,170,174,89) de la sección I.C.
La elección anterior de elementos de la subálgebra de Cartan parece
muy arbitraria; sin embargo, no lo es tanto si se examina con
detenimiento de la tabla 1. Se comprueba en el cuadrante superior
izquierdo de ésta que ![]() ,
, ![]() ,
, ![]() ,
, ![]() , conmutan entre
sí (bajo paréntesis de Poisson); para formar una
subálgebra de Cartan, se deben añadir a los anteriores
elementos todos aquellos tales que la condición de paréntesis
de Poisson nulos entre miembros cualesquiera del conjunto formado
se cumpla; sin embargo, es evidente, por inspección de la tabla
1, que no se puede añadir a este conjunto ninguna otra
, conmutan entre
sí (bajo paréntesis de Poisson); para formar una
subálgebra de Cartan, se deben añadir a los anteriores
elementos todos aquellos tales que la condición de paréntesis
de Poisson nulos entre miembros cualesquiera del conjunto formado
se cumpla; sin embargo, es evidente, por inspección de la tabla
1, que no se puede añadir a este conjunto ninguna otra ![]() ni
ni
![]() , pues la relación de paréntesis de Poisson nulos no se
conserva si se añade alguna. Entonces,
, pues la relación de paréntesis de Poisson nulos no se
conserva si se añade alguna. Entonces, ![]() ,
, ![]() ,
, ![]() ,
,
![]() , junto con sus combinaciones lineales, constituyen una
subálgebra de Cartan. Por inspección del cuadrante inferior
derecho de la tabla 1, se concluye que con los elementos
, junto con sus combinaciones lineales, constituyen una
subálgebra de Cartan. Por inspección del cuadrante inferior
derecho de la tabla 1, se concluye que con los elementos ![]() ,
,
![]() ,
, ![]() ,
, ![]() , se puede construir una subálgebra de
Cartan, lo mismo que con los elementos
, se puede construir una subálgebra de
Cartan, lo mismo que con los elementos ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
sin embargo, se eligió formar la subálgebra de Cartan que se
usaría con combinaciones lineales de
,
sin embargo, se eligió formar la subálgebra de Cartan que se
usaría con combinaciones lineales de ![]() ,
, ![]() ,
, ![]() ,
,
![]() , pues en la sección I.C ya se construyó con ellas en
conjunto de 4 expresiones con significado físico directo;
dicho conjunto de expresiones es el que aparece en las ecs.
(14,17). Que el conjunto (14,17) forma junto con
, pues en la sección I.C ya se construyó con ellas en
conjunto de 4 expresiones con significado físico directo;
dicho conjunto de expresiones es el que aparece en las ecs.
(14,17). Que el conjunto (14,17) forma junto con ![]() (elemento
nulo) una subálgebra, es obvio de su construcción, que dicha
subálgebra es de Cartan se comprueba como sigue [33]:
es nilpotente (por su definición), es su propio
normalizador, se comprueba esto por inspección de la tabla 1:
dada cualquier
(elemento
nulo) una subálgebra, es obvio de su construcción, que dicha
subálgebra es de Cartan se comprueba como sigue [33]:
es nilpotente (por su definición), es su propio
normalizador, se comprueba esto por inspección de la tabla 1:
dada cualquier ![]() distinta de las que forman la subálgebra,
es eigenfunción de alguna de estas últimas, bajo paréntesis
de Poisson; lo mismo sucede con cada
distinta de las que forman la subálgebra,
es eigenfunción de alguna de estas últimas, bajo paréntesis
de Poisson; lo mismo sucede con cada ![]() ; entonces, no existe
una subálgebra que contenga propiamente a la obtenida y en la
cual ésta sea un ideal [33].
; entonces, no existe
una subálgebra que contenga propiamente a la obtenida y en la
cual ésta sea un ideal [33].
Utilizando la tabla 1, se obtiene la tabla de paréntesis de Poisson
de los miembros de la subálgebra de Cartan con las ![]() s y
s y
![]() s (tabla 2).
s (tabla 2).
1pt
| [f,g] | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
|
|
|
|
|
|
|
|
| 0 | |
|
0 | 0 | |
|
0 | 0 | |
|
0 | 0 | |
|
0 | |
| 0 | |
|
0 | 0 | |
|
0 | |
0 | 0 | |
|
0 | 0 | |
|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Como se ve de la tabla 2, todos los eigenvalores son imaginarios. Para obtener eigenvalores reales, se trabajará con los operadores:
| (18) | |||
| (19) | |||
| (20) | |||
| (21) |
El ![]() que aparece en (18) es un factor de normalización adecuado.
que aparece en (18) es un factor de normalización adecuado.
Con estos miembros modificados de la subálgebra de Cartan (ecs. (18-21)), se tiene la siguiente tabla de paréntesis de Poisson (tabla 3):
2pt
| [f,g] | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
|
|
|
|
|
|
|
|
| 0 | |
|
0 | 0 | |
|
0 | 0 |
|
|
0 | 0 | |
|
0 | |
| 0 | |
|
0 | 0 | |
|
0 | |
0 | 0 | |
|
0 | 0 | |
|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
De la tabla 3, se obtienen directamente [33] los siguientes vectores raíces:
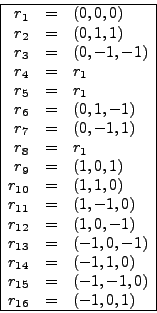
Usando la tabla 4, se construye el diagrama de raíces [33]
(root diagram) del álgebra de Lie que se tiene. Aunque no será usado
más adelante, será incluído aquí pues es una herramienta muy
útil, ya que, por su simple inspección [33], se tiene
prácticamente
toda la información contenida en la tabla 1, o sea, todas las relaciones de
paréntesis de Poisson entre las ![]() s y
s y ![]() s.
s.
Estudiando la tabla 4, se demuestra que:
| (22) | |||
| (23) | |||
| (24) |
Son raíces simples. La comprobación es la siguiente: un subconjunto
![]() del conjunto de vectores raíces está
constituído por raíces simples si y sólo
si [48]:
del conjunto de vectores raíces está
constituído por raíces simples si y sólo
si [48]:
Dados
![]()
| (25) | |||
 |
(26) |
En el caso de ![]() ,
, ![]() ,
, ![]() dados por (22-24), se tienen los siguientes resultados:
dados por (22-24), se tienen los siguientes resultados:
Para ![]() y
y ![]() :
:
| (27) |
Para ![]() y
y ![]() :
:
| (28) |
Para ![]() y
y ![]() :
:
| (29) |
Comparando (27,28,29) con (25,26), se concluye que ![]() ,
, ![]() ,
,
![]() , son raíces simples.
, son raíces simples.
Se demuestra fácilmente [48] que hay sólo 4 ángulos posibles entre vectores raíces simples:
![]() y
y ![]() . Además, sólo hay dos valores distintos (y distintos de 0) posibles para
. Además, sólo hay dos valores distintos (y distintos de 0) posibles para ![]() , siendo
, siendo ![]() una raíz simple; de acuerdo con ésto, se dice que se tienen raíces simples ``largas" y ``cortas", dependiendo del valor de
una raíz simple; de acuerdo con ésto, se dice que se tienen raíces simples ``largas" y ``cortas", dependiendo del valor de ![]() . Usando estas dos características de las raíces simples se construye el diagrama de Schouten del cual se habló anteriormente: se representa una raíz simple por un disco, el cual es blanco (
. Usando estas dos características de las raíces simples se construye el diagrama de Schouten del cual se habló anteriormente: se representa una raíz simple por un disco, el cual es blanco (![]() ) si la raíz es larga y negro (
) si la raíz es larga y negro (![]() ) si la raíz es corta; estos discos se unen por un número de líneas que es función del ángulo
) si la raíz es corta; estos discos se unen por un número de líneas que es función del ángulo ![]() entre las raíces simples correspondientes [48].
entre las raíces simples correspondientes [48].
Si
![]() , los discos no se unen; si
, los discos no se unen; si
![]() , los discos se unen por 1, 2 y 3 líneas, respectivamente.
, los discos se unen por 1, 2 y 3 líneas, respectivamente.
En nuestro caso, de la tabla 4 se demuestra que:
| (30) |
Respecto al ángulo ![]() se tiene que:
se tiene que:
Para ![]() y
y ![]()
| (31) |
Para ![]() y
y ![]()
| (32) |
Para ![]() y
y ![]()
| (33) |
Comparando lo dicho para diagramas de Schouten con los resultados (30-33), se tiene que el diagrama de Schouten es, en nuestro caso:
Este diagrama es el del álgebra de Lie correspondiente al grupo
![]() , ésto parecería indicar que el grupo dinámico
buscado es
, ésto parecería indicar que el grupo dinámico
buscado es ![]() . Sin embargo, según las consideraciones
siguientes, el grupo dinámico resulta ser
. Sin embargo, según las consideraciones
siguientes, el grupo dinámico resulta ser ![]() . (Estos
grupos están muy relacionados, pues
. (Estos
grupos están muy relacionados, pues ![]() es isomorfo al grupo
de matrices
es isomorfo al grupo
de matrices ![]() unitarias: conmutan todas con la
identidad (``matriz métrica");
unitarias: conmutan todas con la
identidad (``matriz métrica"); ![]() es el conjunto de
matrices unitarias
es el conjunto de
matrices unitarias ![]() que conmutan con una matriz
diagonal con dos
que conmutan con una matriz
diagonal con dos ![]() s y dos
s y dos ![]() s, pudiendo representarse la
diagonal de esta matriz así:
s, pudiendo representarse la
diagonal de esta matriz así: ![]() .
.
Todos los elementos del álgebra de Lie del grupo buscado (![]() s y
s y ![]() s)
conmutan, bajo paréntesis de Poisson, con
s)
conmutan, bajo paréntesis de Poisson, con
![]() .
. ![]() define en el espacio
vectorial de las
define en el espacio
vectorial de las
![]() , un operador lineal, a
partir del operador bilineal que son los paréntesis de
Poisson [33]. Se trata, entonces, de diagonalizar este
operador lineal para ver que tipo de ``matriz métrica"
representa su matriz en la base de sus eigenvectores.
Prácticamente, ésto ya está hecho pues, de las fórmulas
(97,98) de la sección I.C, se tiene que las funciones que siguen
((34,35)), son tales que las funciones (34) son eigenvectores de
, un operador lineal, a
partir del operador bilineal que son los paréntesis de
Poisson [33]. Se trata, entonces, de diagonalizar este
operador lineal para ver que tipo de ``matriz métrica"
representa su matriz en la base de sus eigenvectores.
Prácticamente, ésto ya está hecho pues, de las fórmulas
(97,98) de la sección I.C, se tiene que las funciones que siguen
((34,35)), son tales que las funciones (34) son eigenvectores de
![]() (en el sentido mencionado arriba) con
eigenvalor
(en el sentido mencionado arriba) con
eigenvalor ![]() , mientras que las funciones (35) lo son
con eigenvalor
, mientras que las funciones (35) lo son
con eigenvalor ![]() :
:
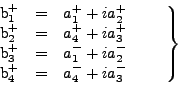 |
(34) |
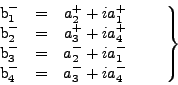 |
(35) |
Entonces, la diagonal de la matriz asociada a ![]() en la base
en la base
![]() se puede escribir en la
forma:
se puede escribir en la
forma:
![]() . Ya que el factor
. Ya que el factor ![]() aparece en todos
los eigenvalores, es irrelevante, por lo que se puede trabajar con
el operador
aparece en todos
los eigenvalores, es irrelevante, por lo que se puede trabajar con
el operador ![]()
![]()
![]() , y se tiene que todos los elementos del álgebra
de Lie también conmutan con
, y se tiene que todos los elementos del álgebra
de Lie también conmutan con ![]()
![]() bajo
paréntesis de Poisson. En la base
bajo
paréntesis de Poisson. En la base
![]() ,
,
![]()
![]() tiene asociada una matriz diagonal cuya
diagonal se puede escribir en la forma:
tiene asociada una matriz diagonal cuya
diagonal se puede escribir en la forma:
![]() . Esta matriz
. Esta matriz ![]() sobre el espacio de los reales se
puede hacer corresponder con una matriz
sobre el espacio de los reales se
puede hacer corresponder con una matriz ![]() sobre el
espacio de los complejos, la cual es diagonal, pudiéndose
representar su diagonal en la forma:
sobre el
espacio de los complejos, la cual es diagonal, pudiéndose
representar su diagonal en la forma:
![]() , siendo 1 = (1,1) y -1 = (-1,-1),
números complejos. Desde este punto de vista, los elementos del
álgebra de Lie forman un álgebra isomorfa a la correspondiente
al grupo de matrices en este espacio complejo de 4 dimensiones que
conmutan con la ``matriz métrica"
, siendo 1 = (1,1) y -1 = (-1,-1),
números complejos. Desde este punto de vista, los elementos del
álgebra de Lie forman un álgebra isomorfa a la correspondiente
al grupo de matrices en este espacio complejo de 4 dimensiones que
conmutan con la ``matriz métrica"
![]() . Entonces, el grupo de Lie que es grupo
dinámico o de no-invariancia para nuestro problema es,
efectivamente,
. Entonces, el grupo de Lie que es grupo
dinámico o de no-invariancia para nuestro problema es,
efectivamente, ![]() .
.