En unidades Gaussianas, el Lagrangiano para el problema de una partícula
con carga eléctrica ![]() moviéndose en una región donde existen un
potencial escalar
moviéndose en una región donde existen un
potencial escalar ![]() y uno vectorial
y uno vectorial ![]() está dado por [15]:
está dado por [15]:
| (1) |
En la ec. (1),
![]() es la energía cinética de la
partícula móvil.
es la energía cinética de la
partícula móvil.
Por el procedimiento habitual [16], se obtiene el Hamiltoniano
correspondiente (suponiendo que ![]() no depende de velocidades):
no depende de velocidades):
Para el problema que se tiene, en el cual el potencial escalar
correspondería al debido a una carga eléctrica de magnitud ![]() en
el monopolo, se debería tener:
en
el monopolo, se debería tener:
En la ec. (1-b), ![]() es la magnitud del vector
es la magnitud del vector ![]() que une
al monopolo electromagnético con la partícula móvil; para un
sistema cartesiano con origen en dicho monopolo,
que une
al monopolo electromagnético con la partícula móvil; para un
sistema cartesiano con origen en dicho monopolo,
![]() .
.
Sin embargo, usando el potencial (1-b), la ecuación de Hamilton-Jacobi no es separable en las coordenadas cuadrático parabólicas empleadas (de hecho, no es separable en coordenadas conocidas (esféricas, parabólicas, cuaterniónicas). Como lo que interesaba era estudiar la simetría del problema usando un método que descansa en el uso de coordenadas de acción-ángulo, o sea, en la separabilidad de la ec. de Hamilton-Jacobi, se usó el potencial escalar:
En la ec. (1-c),
![]() ,
siendo
,
siendo ![]() la carga
magnética del monopolo.
la carga
magnética del monopolo.
El problema parace ser, entonces, poco realista, pues para
![]() pequeña el término
pequeña el término
![]() es el más importante en 1-c.
Sin embargo, cuando
es el más importante en 1-c.
Sin embargo, cuando ![]() crece, el más importante es
crece, el más importante es
![]() .
.
Se dirá en lo siguiente un poco más sobre la influencia de
![]() en el Hamiltoniano.
en el Hamiltoniano.
Sea ![]() el Hamiltoniano obtenido de (1-a) al incluir el potencial
(1-b). Sea
el Hamiltoniano obtenido de (1-a) al incluir el potencial
(1-b). Sea ![]() el obtenido de incluir (1-c) en (1-a). Se
sabe [17] que, para un sistema dado, el Hamiltoniano genera
una transformación canónica infinitesimal que describe el
cambio infinitesimal de coordenadas y momenta en el tiempo; por
aplicación sucesiva de esta transformación, con el tiempo como
parámetro, se genera el desarrollo (movimiento) del sistema con
el tiempo en el espacio fase. Desde este punto de vista, se puede
decir que el Hamiltoniano general el movimiento del sistema en el
tiempo, a partir de las condiciones iniciales. Supóngase que a
un tiempo
el obtenido de incluir (1-c) en (1-a). Se
sabe [17] que, para un sistema dado, el Hamiltoniano genera
una transformación canónica infinitesimal que describe el
cambio infinitesimal de coordenadas y momenta en el tiempo; por
aplicación sucesiva de esta transformación, con el tiempo como
parámetro, se genera el desarrollo (movimiento) del sistema con
el tiempo en el espacio fase. Desde este punto de vista, se puede
decir que el Hamiltoniano general el movimiento del sistema en el
tiempo, a partir de las condiciones iniciales. Supóngase que a
un tiempo ![]() a partir del tiempo
a partir del tiempo ![]() al cual se dan las
condiciones iniciales,
al cual se dan las
condiciones iniciales, ![]() , de acuerdo con lo que se acaba de
decir, da lugar a una trayectoria (que será la del sistema
real). Como, cuando
, de acuerdo con lo que se acaba de
decir, da lugar a una trayectoria (que será la del sistema
real). Como, cuando ![]() ,
, ![]() se espera cierto
tipo de continuidad, en el sentido de que, si el movimiento tiene
lugar de tal manera que
se espera cierto
tipo de continuidad, en el sentido de que, si el movimiento tiene
lugar de tal manera que ![]() siempre es grande (por condiciones
iniciales apropiadas), la trayectoria en el espacio fase generada
por
siempre es grande (por condiciones
iniciales apropiadas), la trayectoria en el espacio fase generada
por ![]() debe ser muy parecida (cercana en cada punto) a la
generada por
debe ser muy parecida (cercana en cada punto) a la
generada por ![]() . O sea, para
. O sea, para ![]() grande, se espera que
grande, se espera que ![]() describa con buena aproximación al problema real. Los argumentos
anteriores se basan en consideraciones de estabilidad de las
ecuaciones canónicas, las cuales no se demostraron por su
dificultad y porque no se usará dicha demostración más
adelante.
describa con buena aproximación al problema real. Los argumentos
anteriores se basan en consideraciones de estabilidad de las
ecuaciones canónicas, las cuales no se demostraron por su
dificultad y porque no se usará dicha demostración más
adelante.
Desde otro punto de vista, de acuerdo con el teorema de órbitas
revolventes de Newton [18], el efecto del término
![]() es causar
una precesión de la órbita ( ya que
es causar
una precesión de la órbita ( ya que
![]() , se tendrá un retardamiento). Es claro que, para pequeñas
cargas magnéticas, la interacción de tipo magnético podrá
tratarse como una perturbación de la puramente coulómbica, en
cuyo caso, efectivamente, el único efecto de
, se tendrá un retardamiento). Es claro que, para pequeñas
cargas magnéticas, la interacción de tipo magnético podrá
tratarse como una perturbación de la puramente coulómbica, en
cuyo caso, efectivamente, el único efecto de
![]() en el
movimiento total será una precesión de la órbita de la
partícula móvil, la cual es casi plana para
en el
movimiento total será una precesión de la órbita de la
partícula móvil, la cual es casi plana para ![]() pequeña, de acuerdo con las fórmulas (7,9) de la sección
I-B.
pequeña, de acuerdo con las fórmulas (7,9) de la sección
I-B.
Otra de las razones por las cuales se introduce el término
![]() es la
siguiente: el Hamiltoniano del problema de Coulomb en coordenadas
plano polares
es la
siguiente: el Hamiltoniano del problema de Coulomb en coordenadas
plano polares ![]() se puede escribir en la
forma [19]:
se puede escribir en la
forma [19]:
Sin embargo, en coordenadas esféricas
![]() ,
se puede escribir el Hamiltoniano (1-a) en la forma [20]:
,
se puede escribir el Hamiltoniano (1-a) en la forma [20]:
Entonces, se ve que, si ![]() (dado por la ec. (7) de
la sección 1-B), va a tomar el papel de
(dado por la ec. (7) de
la sección 1-B), va a tomar el papel de ![]() para el
problema tradicional de Coulomb, al emplear
para el
problema tradicional de Coulomb, al emplear ![]() dado por (1-c) en
(1-e), se obtiene una expresón análoga a (1-d), por lo que se
espera encontrar, en este caso, el mismo tipo de simetría que
en el problema de Coulomb.
dado por (1-c) en
(1-e), se obtiene una expresón análoga a (1-d), por lo que se
espera encontrar, en este caso, el mismo tipo de simetría que
en el problema de Coulomb.
Entonces, el Hamiltoniano que se estudiará es:
| (2) |
Como se dijo en la Introducción, se usará el potencial vectorial:
Se basará la discusión en el uso de coordenadas paraboloidales o
cuadrático-parabólicas
![]() , definidas por:
, definidas por:
| (3) | |||
| (4) | |||
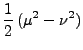 |
(5) |
Un interés esencial que existe para usar estas coordenadas consiste
en que son tales que las superficies
![]() &
&
![]() son simétricas con respecto a rotaciones que tengan
como eje al eje Z. como se vió en la Introducción, este eje es
muy especial, pues se escogió el sistema de coordenadas de tal
manera que el eje Z tiene la dirección del vector
son simétricas con respecto a rotaciones que tengan
como eje al eje Z. como se vió en la Introducción, este eje es
muy especial, pues se escogió el sistema de coordenadas de tal
manera que el eje Z tiene la dirección del vector ![]() que aparece en
que aparece en ![]() (fórmula (13) Introducción); o
viceversa, dado el sistema coordenado [x, y, z,] se escogió
(fórmula (13) Introducción); o
viceversa, dado el sistema coordenado [x, y, z,] se escogió
![]() tal que tuviera la dirección del eje Z. Lo anterior
se refleja en la forma tan simple en que depende
tal que tuviera la dirección del eje Z. Lo anterior
se refleja en la forma tan simple en que depende ![]() de
de
![]() , el expresarse en las nuevas coordenadas (o sea, al
expresar sus componentes Ax,Ay,Az en las nuevas coordenadas);
también, cuando
, el expresarse en las nuevas coordenadas (o sea, al
expresar sus componentes Ax,Ay,Az en las nuevas coordenadas);
también, cuando ![]() se expresa, digamos, en coordenadas
esféricas
se expresa, digamos, en coordenadas
esféricas
![]() (se le considera como un vector
y se le somete a un cambio de coordenadas), se obtienen las
siguientes componentes, teniendo
(se le considera como un vector
y se le somete a un cambio de coordenadas), se obtienen las
siguientes componentes, teniendo ![]() el mismo significado
geométrico que en las coordenadas
cuadrático-parabólicas [21].
el mismo significado
geométrico que en las coordenadas
cuadrático-parabólicas [21].
Además, al usar estas coordenadas, se obtiene, expresando al
Hamiltoniano en función de ellas, una expresión
remarcablemente simétricas (ec. (17)), la cual facilita la
determinación de su grupo de simetría. Se comprueba
directamente que, usando ![]() (ec. (14) Introducción), el
Hamiltoniano obtenido en estas coordenadas pierde bastante de su
simetría funcional.
(ec. (14) Introducción), el
Hamiltoniano obtenido en estas coordenadas pierde bastante de su
simetría funcional.
Se dará ahora la interpretación geométrica de las coordenadas que se usarán. De las ecs. (3,4,5):
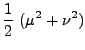 |
(6) | ||
| (7) | |||
| (8) |
De las ecs. (7, 8), introduciendo
![]() , se obtiene:
, se obtiene:
| (9) |
| (10) |
Para cada valor de ![]() , la ec. (9) es la de una parábola con foco en
, la ec. (9) es la de una parábola con foco en
![]() , vértice en
, vértice en
![]() , con eje
, con eje ![]() y que se
abre hacia la izquierda. Para cada valor de
y que se
abre hacia la izquierda. Para cada valor de ![]() , la ec. (10) es
la de una parábola con foco en
, la ec. (10) es
la de una parábola con foco en ![]() , vértice en
, vértice en
![]() , eje el eje
, eje el eje ![]() y que se abre hacia la derecha.
Entonces, al variar los parámetros
y que se abre hacia la derecha.
Entonces, al variar los parámetros ![]() y
y ![]() , se obtiene un
conjunto de parábolas (estrictamente, media parábolas, pues
, se obtiene un
conjunto de parábolas (estrictamente, media parábolas, pues ![]() ), confocales en el origen (
), confocales en el origen (![]() ). Como el análisis
anterior es válido para cualquier plano
). Como el análisis
anterior es válido para cualquier plano
![]() , es
claro que, al variar
, es
claro que, al variar
![]() , se
obtendrá, en 3 dimensiones, un conjunto de paraboloides de
revolución confocales en el origen que ``barren" todo el
espacio.
, se
obtendrá, en 3 dimensiones, un conjunto de paraboloides de
revolución confocales en el origen que ``barren" todo el
espacio.
Entonces, para localizar geométricamente el punto
Se pasará ahora de la descripción (ec. (2)) en términos de las
coordenadas y momenta canónicos
![]() a
otra en términos de coordenadas
a
otra en términos de coordenadas
![]() y momenta
canónicos
y momenta
canónicos
![]() por medio de una
transformación canónica con función generadora [12]:
por medio de una
transformación canónica con función generadora [12]:
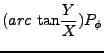 |
(11) |
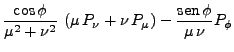 |
(12) | ||
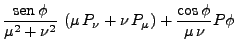 |
(13) | ||
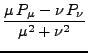 |
(14) |
Para el potencial ![]() se tiene que:
se tiene que:
| (15) |
Entonces ![]() , obtenido de introducir (1-b) en la ec. (1-a), toma la
siguiente forma en este nuevo conjunto canónico:
, obtenido de introducir (1-b) en la ec. (1-a), toma la
siguiente forma en este nuevo conjunto canónico:
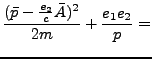 |
|||
![$\displaystyle \frac{(\mu^2 + \nu^2)^{-1}}{2m}\Big[ P^2_\mu + P^2_\nu + \frac{(P_\phi - \varepsilon)^2}{\mu^2} + \frac{(P_\phi + \varepsilon)^2}{\nu^2}\Big] +$](img265.png) |
|||
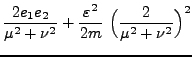 |
(16) |
Es aquí donde se ve la necesidad de trabajar con
![]() ,
pues, debido a la presencia de
,
pues, debido a la presencia de
![]() en un denominador en la ec. (16),
la ecuación de Hamilton-Jacobi correspondiente no es separable en estas coordenadas cuadrático-parabólicas.
en un denominador en la ec. (16),
la ecuación de Hamilton-Jacobi correspondiente no es separable en estas coordenadas cuadrático-parabólicas.
Entonces:
| (17) |
De la ec. (17) es aparente la simetría funcional del Hamiltoniano cuando se expresa en términos de las coordenadas que se están usando.
La ecuación de Hamilton-Jacobi para (17) es [23]:
| (18) |
Ya que ![]() no depende explícitamente de
no depende explícitamente de ![]() ni de
ni de ![]() (ec. 17), se
puede probar como solución a la ec. (18) la función [24]:
(ec. 17), se
puede probar como solución a la ec. (18) la función [24]:
| (19) |
Con
![]() y
y
![]() = energía total del
sistema, pues los potenciales (escalar y vectorial) no dependen de
velocidades y las ecuaciones de transformación (3,4,5) no contienen al
tiempo explícitamente [25]. De las ec. (18,19):
= energía total del
sistema, pues los potenciales (escalar y vectorial) no dependen de
velocidades y las ecuaciones de transformación (3,4,5) no contienen al
tiempo explícitamente [25]. De las ec. (18,19):
| (20) |
La ecuación diferencial (20) se puede separar de las siguiente manera:
| (21) |
| (22) |
Siendo ![]() la constante de separación.
Haciendo
la constante de separación.
Haciendo
![]() ,
,
![]() , (21) y (22) se convierten en:
, (21) y (22) se convierten en:
| (23) |
| (24) |
Con ![]() . Las expresiones (23) y (24) corresponden formalmente a
Hamiltonianos de dos osciladores armónicos, lo que será más
aparente al introducir nuevas coordenadas en (23) y (24) por medio
de las siguientes funciones generadoras [22]:
. Las expresiones (23) y (24) corresponden formalmente a
Hamiltonianos de dos osciladores armónicos, lo que será más
aparente al introducir nuevas coordenadas en (23) y (24) por medio
de las siguientes funciones generadoras [22]:
Para (23), sea
![]() y sea
y sea ![]() su
variable canónicamente conjugada; sea la función generadora:
su
variable canónicamente conjugada; sea la función generadora:
| (25) |
Entonces: [22]
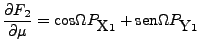 |
(26) | ||
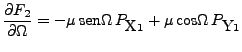 |
(27) | ||
 |
(28) | ||
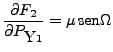 |
(29) |
Entonces, ![]() queda en la forma:
queda en la forma:
| (30) |
Similarmente, para (24), definiendo
![]() con
con ![]() su variable canónica conjugada y usando la función generadora:
su variable canónica conjugada y usando la función generadora:
| (31) |
se llega a la expresión:
| (32) |
Las expresiones (30,32) son formalmente idénticas, para
![]() a los Hamiltonianos de osciladores
armónicos bidimensionales isotrópicos [26] con
constantes de fuerza
a los Hamiltonianos de osciladores
armónicos bidimensionales isotrópicos [26] con
constantes de fuerza ![]() idénticas. La simetría
del oscilador armónico bidimensional ha sido estudiada en forma
completa [26], resultando ser que su grupo de simetría
es
idénticas. La simetría
del oscilador armónico bidimensional ha sido estudiada en forma
completa [26], resultando ser que su grupo de simetría
es
![]() . Esto sugiere que el grupo de simetría
para
. Esto sugiere que el grupo de simetría
para ![]() está relacionado con
está relacionado con
![]() . Sin
embargo, hay algunas dificultades para establecer esta relación:
. Sin
embargo, hay algunas dificultades para establecer esta relación:
![]() &
& ![]() no son funciones independientes, pues
de su definición, se tiene que:
no son funciones independientes, pues
de su definición, se tiene que:
| (33) |
Otra dificultad, que impide obtener los generadores del grupo de
simetría del Hamiltoniano H a partir directamente de los
dados en la ref. [26], consiste en que, en esta última, la
construcción de los generadores de ![]() se hace basándose
en expresiones del tipo:
se hace basándose
en expresiones del tipo:
Sin embargo, según se verá más adelante (ec. 80), las cantidades correspondientes obtenidas para H son del tipo:
El procedimiento que se sigue en la obtención del grupo
de simetría de ![]() es el siguiente: se define un nuevo
momento
es el siguiente: se define un nuevo
momento
![]() en
en ![]() , siendo
, siendo ![]() su
variable canónica conjugada. Esto equivale a trabajar en un
espacio fase de 8 dimensiones, siendo de 6 el apropiado al
problema; o sea, implica el uso de multiplicadores de
Lagrange [17], lo cual, de hacerse, complicaría todas
las ecuaciones; para evitar lo anterior, se tratará a
su
variable canónica conjugada. Esto equivale a trabajar en un
espacio fase de 8 dimensiones, siendo de 6 el apropiado al
problema; o sea, implica el uso de multiplicadores de
Lagrange [17], lo cual, de hacerse, complicaría todas
las ecuaciones; para evitar lo anterior, se tratará a ![]() y
y
![]() como otras variables canónicas independientes. Con
ésto, se facilita la introducción de variables de
acción-ángulo, por la simetría que adquiere el ``nuevo
Hamiltoniano" (ec. 52); como
como otras variables canónicas independientes. Con
ésto, se facilita la introducción de variables de
acción-ángulo, por la simetría que adquiere el ``nuevo
Hamiltoniano" (ec. 52); como ![]() es cíclica en el
``nuevo''
es cíclica en el
``nuevo'' ![]()
![]() ,
ésto no acarrea problemas. Ya que el ``nuevo
,
ésto no acarrea problemas. Ya que el ``nuevo ![]() '' es función
sólo de la suma de las variables de acción-ángulo, es
aplicable un procedimiento debido a V. A. Dulock y H. V.
McIntosh [28] para hallar las constantes del movimiento, el
cual depende de este hecho. Del conjunto de constantes del
movimiento obtenidos se escogen como aceptables sólo aquellas
tales que sus paréntesis de Poisson con
'' es función
sólo de la suma de las variables de acción-ángulo, es
aplicable un procedimiento debido a V. A. Dulock y H. V.
McIntosh [28] para hallar las constantes del movimiento, el
cual depende de este hecho. Del conjunto de constantes del
movimiento obtenidos se escogen como aceptables sólo aquellas
tales que sus paréntesis de Poisson con ![]() sean 0. La
razón para ésto es la siguiente:
sean 0. La
razón para ésto es la siguiente:
El movimiento debe tener
lugar en el hiperplano del espacio fase cuya ecuación es:
![]() Cada
constante del movimiento,
Cada
constante del movimiento, ![]() , es una función de las coordenadas
y momenta canónicas que genera una transformación canónica
infinitesimal tal que [29]:
, es una función de las coordenadas
y momenta canónicas que genera una transformación canónica
infinitesimal tal que [29]:
siendo ![]() el parámetro de la transformación
infinitesimal y
el parámetro de la transformación
infinitesimal y ![]() cualquier función de las variables y
momenta canónicos. Siendo
cualquier función de las variables y
momenta canónicos. Siendo
![]() los
cambios de las variables y momenta canónicas producidos por la
transformación, se tiene que [29]:
los
cambios de las variables y momenta canónicas producidos por la
transformación, se tiene que [29]:
En particular, para
![]() , se
tiene que el cambio de
, se
tiene que el cambio de ![]() producido por la
transformación infinitesimal generada por
producido por la
transformación infinitesimal generada por ![]() está dado por:
está dado por:
Como el movimiento del sistema real es tal que en el espacio fase se
está restringido al hiperplano
![]() , se
debe tener que, para cualquier transformación del sistema,
, se
debe tener que, para cualquier transformación del sistema,
![]() . Entonces, cuando esta
transformación corresponde a una del tipo que se está
tratando, de la fórmula de arriba, se tiene que, siendo
. Entonces, cuando esta
transformación corresponde a una del tipo que se está
tratando, de la fórmula de arriba, se tiene que, siendo ![]() arbitrario:
arbitrario:
Es importante notar que el Hamiltoniano en un espacio fase
de 8 dimensiones del que se habló anteriormente, no corresponde
a un sistema físico análogo al original, con la única
diferencia de que ahora ![]() sea variable con el tiempo,
pues un sistema así no puede existir en la naturaleza, si se
aceptan como verdaderas las ecuaciones de Maxwell generalizadas
dadas por las ecs. (3) de la introducción. Es sencillo demostrar
que estas ecuaciones implican las leyes de conservación de las
cargas eléctricas y magnéticas, en forma de las ecuaciones de
continuidad:
sea variable con el tiempo,
pues un sistema así no puede existir en la naturaleza, si se
aceptan como verdaderas las ecuaciones de Maxwell generalizadas
dadas por las ecs. (3) de la introducción. Es sencillo demostrar
que estas ecuaciones implican las leyes de conservación de las
cargas eléctricas y magnéticas, en forma de las ecuaciones de
continuidad:
Entonces, sí
![]()
ó
Siguiendo el programa que se acaba de trazar, se cambiará de las
coordenadas
Entonces [22]:
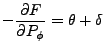 |
(34) | ||
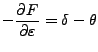 |
(35) | ||
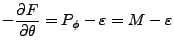 |
(36) | ||
 |
(37) |
De las ecuaciones (17,36,37):
| (38) |
Se introducirá ahora un sistema de coordenadas canónicas
![]() en el cual
la ecuación de Hamilton-Jacobi es separable (completamente) de
una manera uniforme: el mismo tipo de ecuación diferencial se
obtiene para cada coordenada; esto es con el objeto de calcular
las variables de acción y ángulo. Sea la función generadora:
en el cual
la ecuación de Hamilton-Jacobi es separable (completamente) de
una manera uniforme: el mismo tipo de ecuación diferencial se
obtiene para cada coordenada; esto es con el objeto de calcular
las variables de acción y ángulo. Sea la función generadora:
| (39) |
Entonces:
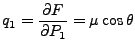 |
(40) | ||
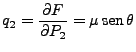 |
(41) | ||
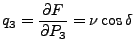 |
(42) | ||
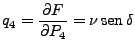 |
(43) |
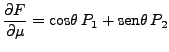 |
(44) | ||
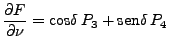 |
(45) | ||
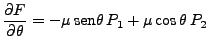 |
(46) | ||
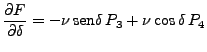 |
(47) |
De las ecuaciones (44-47):
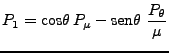 |
(48) | ||
 |
(49) | ||
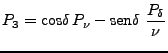 |
(50) | ||
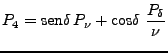 |
(51) |
Las ecuaciones (40-43) y (42-50) servirán para regresar,
posteriormente, al sistema
![]() .
.
En las nuevas coordenadas, el Hamiltoniano toma la forma:
| (52) |
La ecuación de Hamilton-Jacobi correspondiente es:
| (53) |
Se propone una solución del tipo [24]:
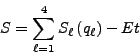 |
(54) |
De (53) y (54):
![\begin{displaymath}
\frac{1}{2m \sum_{\ell = 1}^4 q^2_\ell} \Big[\sum_{\ell...
...
\Big(\frac{dS_\ell}{dq_\ell}\Big)^2 + 4me_1 e_2\Big] - E = 0
\end{displaymath}](img365.png) |
(55) |
La ecuación (55) es separable en la forma:
| (56) |
Con
![]() de separación
(nuevos momenta)
de separación
(nuevos momenta)
| (57) |
El momento ![]() es igual a
es igual a
![]() .
.
Las ecuaciones (56) y (57) equivalen a:
| (58) |
| (59) |
Como se está trabajando con coordenadas y momenta reales, se debe tener:
Para
![]() :
:
| (60) |
| (61) |
Si ![]() , o sea, si
, o sea, si ![]() , es claro que de (61) no se pueden
obtener cotas para
, es claro que de (61) no se pueden
obtener cotas para ![]() o sea, no se puede obtener un rango
de variación finito para
o sea, no se puede obtener un rango
de variación finito para ![]() , por lo que, tomando en cuenta
a (58), se ve que es imposible obtener un movimiento periódico.
Esto impone la restricción (importante)
, por lo que, tomando en cuenta
a (58), se ve que es imposible obtener un movimiento periódico.
Esto impone la restricción (importante) ![]() para movimiento
acotado, la cual ya fue hallada cuando se separó la ecuación
de Hamilton-Jacobi en dos ecuaciones que correspondían
formalmente a Hamiltonianos de osciladores armónicos
bidimensionales (ecs. (23,24)). Entonces, para
para movimiento
acotado, la cual ya fue hallada cuando se separó la ecuación
de Hamilton-Jacobi en dos ecuaciones que correspondían
formalmente a Hamiltonianos de osciladores armónicos
bidimensionales (ecs. (23,24)). Entonces, para ![]() , de (61):
, de (61):
| (62) |
Lo cual implica que
![]() . Entonces de (62):
. Entonces de (62):
| (63) |
| (64) |
O sea, se obtiene un movimiento de tipo libratorio. [30]
Para ![]() , se tiene:
, se tiene:
| (65) |
Ya que ![]() , entonces:
, entonces:
| (66) |
Esto implica que
![]() , o sea, que:
, o sea, que:
| (67) |
Pero, según lo que se demostró para
![]() .
Entonces,
.
Entonces,
![]() . Esto implica otra importante restricción (no
muy independiente de
. Esto implica otra importante restricción (no
muy independiente de ![]() ) para tener movimiento periódico:
las cargas
) para tener movimiento periódico:
las cargas ![]() y
y ![]() deben ser de signos contrarios
(para que se pueda cumplir que
deben ser de signos contrarios
(para que se pueda cumplir que
![]() ).
).
De la ecuación (66):
| (68) |
Resumiendo se ha obtenido un movimiento de tipo libratorio en el
espacio fase
![]() imponiendo
las restricciones
imponiendo
las restricciones ![]() y
y ![]() de signos opuestos.
de signos opuestos.
Ahora, se calcularán las variables de acción [30]:
Para
![]() :
:
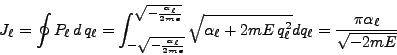 |
(69) |
Para ![]() , por un procedimiento análogo se obtiene;
, por un procedimiento análogo se obtiene;
| (70) |
Es obvio de (69) y (70) que:
| (71) |
O sea que:
| (72) |
Es claro de la ec. anterior que las frecuencias del movimiento son
todas iguales [30], o sea, el movimiento es completamente degenerado.
Estas frecuencias están dadas, para
![]() por [30]:
por [30]:
Los períodos están dados, con
![]() , por:
, por:
Esta última expresión es idéntica a la que se tiene para el problema de Kepler [31].
La relación (72) es fundamental en todo lo que sigue, pues, como ya
se dijo anteriormente, el procedimiento de Dulock-McIntosh depende de la
condición [28]
![]() .
.
Debido a que serán usadas más adelante, se calcularán ahora las
variables de ángulo ![]()
![]() se tiene que:
se tiene que:
| (73) |
Con
![]() función característica de Hamilton:
función característica de Hamilton:
De las ecuaciones (56, 59, 69, 70,72):
| (74) |
Con
![]() . Sean:
. Sean:
| (75) |
| (76) |
Entonces, de (73, 76) (para raíces de A y B se tomará siempre el
signo positivo, o sea,
![]() :
:
![$\displaystyle \frac{\partial W}{\partial J_\ell} = \frac{\partial}{\partial J_\...
... \left[\sum^4_{k=1} \int \frac{(AJ J_k - Bq^2_k)^\frac{1}{2}}{J} dq_k\right] =$](img416.png) |
|||
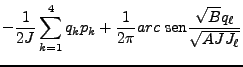 |
(77) |
O sea:
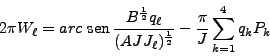 |
(78) |
Lo anterior para
![]() . En la integración (77), se
despreciaron constantes de integración.
. En la integración (77), se
despreciaron constantes de integración.
Siguiendo el procedimiento de Dulock-McIntosh, se introducirán ahora
nuevas coordenadas
![]() con
con
![]() dadas por:
dadas por:
| (79) |
Se pueden poner estas coordenadas en función de las
![]() usando
las ecs. (58, 59, 69, 70, 71, 78 ). Después de una manipulación algebraica
se llega a la expresión:
usando
las ecs. (58, 59, 69, 70, 71, 78 ). Después de una manipulación algebraica
se llega a la expresión:
![$\displaystyle [2(-2mE)^\frac{1}{2}]^{-\frac{1}{2}}
[(-2mE)^\frac{1}{2} q_\ell \...
...arge
e}}^{\pm\pi i B^{-\frac{1}{2}}(-2mE)^{-\frac{1}{2} \sum^4_{k=1}
q_k P_k}}]$](img425.png) |
(80) |
Anteriormente, se dijo que no se podían obtener los generadores del
grupo de simetría buscado, a partir de los dados en la
referencia (26). Las funciones en las cuales, según se dijo, se
basa la construcción de los generadores, son las ![]() dadas por (79,80). La función de que se hablaba está dada,
según es aparente de la ec. (80), por:
dadas por (79,80). La función de que se hablaba está dada,
según es aparente de la ec. (80), por:
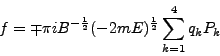
Las coordenadas ![]() introducidas no forman un conjunto
canónico bajo la definición usual de éste [32], aunque
no están muy lejos de formarlo pues se demuestra directamente,
usando la ec. (19), que sus paréntesis de Poisson están dados por:
introducidas no forman un conjunto
canónico bajo la definición usual de éste [32], aunque
no están muy lejos de formarlo pues se demuestra directamente,
usando la ec. (19), que sus paréntesis de Poisson están dados por:
| (81) | |||
| (82) | |||
| (83) |
Estas coordenadas ![]() son eigenfunciones de
son eigenfunciones de ![]() con
eigenvalores tales que, si
con
eigenvalores tales que, si ![]() es eigenvalor correspondiente
a
es eigenvalor correspondiente
a
![]() lo es de
lo es de ![]() (en nuestro caso,
(en nuestro caso,
![]() ). Las
). Las ![]() son eigenfunciones
de
son eigenfunciones
de ![]() tomado como operador lineal obtenido del operador bilineal
que son los paréntesis de Poisson, de la siguiente manera [33]:
tomado como operador lineal obtenido del operador bilineal
que son los paréntesis de Poisson, de la siguiente manera [33]:
| (85) |
El dominio de ![]() es, nuestro caso, el espacio generado
por las
es, nuestro caso, el espacio generado
por las
![]() .
.
Entonces [33,26], los productos de la forma
![]() conmutan con el Hamiltoniano bajo la operación de paréntesis de Poisson, o sea :
conmutan con el Hamiltoniano bajo la operación de paréntesis de Poisson, o sea :
| (86) |
Por lo tanto,
![]() son constantes del movimiento. Existen 16 de ellas.
son constantes del movimiento. Existen 16 de ellas.
 |
(87) |
Sin embargo, según lo que se discutió anteriormente, sólo
serán constantes del movimiento aceptables aquellas
combinaciones de las expresiones (87) que conmuten con
![]() (bajo la operación de paréntesis de Poisson), o
sea, sólo aquellas combinaciones de
(bajo la operación de paréntesis de Poisson), o
sea, sólo aquellas combinaciones de
![]() que
conserven la carga magnética, en el sentido mencionado
anteriormente.
que
conserven la carga magnética, en el sentido mencionado
anteriormente.
Usando las ecuaciones (72, 79, 80, 40-47, 36-37), se demuestra que:
| (88) |
| (89) |
Para calcular los paréntesis de Poisson necesarios, se tomará a
![]() como operador [33] en el espacio de
las
como operador [33] en el espacio de
las ![]() , con el objeto de encontrar sus eigenfunciones y
tratar de construir así las constantes de movimiento
(combinaciones lineales de términos de la forma
, con el objeto de encontrar sus eigenfunciones y
tratar de construir así las constantes de movimiento
(combinaciones lineales de términos de la forma ![]()
![]() ) que conmuten (bajo paréntesis de Poisson) con él.
Para calcular paréntesis de Poisson de funciones de las
) que conmuten (bajo paréntesis de Poisson) con él.
Para calcular paréntesis de Poisson de funciones de las
![]() , hay que tener en cuenta que no forman una base
canónica, por lo que hay que expresarlas primero en función de
una base canónica (los paréntesis de Poisson son
invariantes [32] bajo transformaciones canónicas, o sea,
bajo el cambio de una base canónica a otra). Sin embargo, se
puede evitar este cambio tomando ventaja de las relaciones
(81-83). En una base canónica
, hay que tener en cuenta que no forman una base
canónica, por lo que hay que expresarlas primero en función de
una base canónica (los paréntesis de Poisson son
invariantes [32] bajo transformaciones canónicas, o sea,
bajo el cambio de una base canónica a otra). Sin embargo, se
puede evitar este cambio tomando ventaja de las relaciones
(81-83). En una base canónica
![]() el
paréntesis de Poisson de
el
paréntesis de Poisson de ![]() y
y ![]() está definido por:
está definido por:
| (90) |
Tomando en cuenta las relaciones (81-83) se demuestra, usando la regla de la cadena, que:
| (91) |
con
| (92) |
Esto da un método muy cómodo para calcular los paréntesis de
Poisson de funciones expresadas en términos de las
![]() . En nuestro caso, la ec. (91) es particularmente
útil, pues se está tratando con funciones muy sencillas que
las
. En nuestro caso, la ec. (91) es particularmente
útil, pues se está tratando con funciones muy sencillas que
las ![]() . Usando (91), se demuestra que el operador
. Usando (91), se demuestra que el operador
![]() actúa sobre la base
actúa sobre la base
![]() de la siguiente manera:
de la siguiente manera:
| (93) |
| (94) |
| (95) |
| (96) |
Es obvio de las relaciones (93-96) que los planos generados
por
![]() y
y
![]() son subespacios invariantes de
son subespacios invariantes de
![]() . Entonces, en dichos planos hay
que buscar los eigenvectores (eigenfunciones) de
. Entonces, en dichos planos hay
que buscar los eigenvectores (eigenfunciones) de
![]() . Usando (93-96), se demuestra que los
eigenvectores de
. Usando (93-96), se demuestra que los
eigenvectores de
![]() son:
son:
Con eigenvalor ![]() :
:
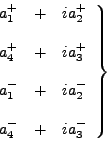 |
(97) |
Con eigenvalor ![]() :
:
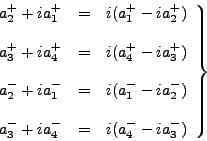 |
(98) |
Con eigenvalor ![]() :
:
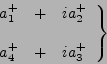 |
(99) |
Con eigenvalor ![]() :
:
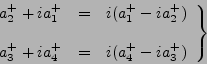 |
(100) |
Es claro [33,26], entonces, que cualquier función de productos de términos (97) con términos (98) conmuta (bajo paréntesis de Poisson) con
![]() . Sin embargo, sólo se pueden escoger productos que den lugar a términos de la forma
. Sin embargo, sólo se pueden escoger productos que den lugar a términos de la forma ![]() que son los que conmutan con
que son los que conmutan con ![]() son nuestras constantes del movimiento. Así, por ejemplo, no se pueden tomar productos de términos marcados (99) con los marcados (100). Existen 8 productos independientes de términos (97) con (98):
son nuestras constantes del movimiento. Así, por ejemplo, no se pueden tomar productos de términos marcados (99) con los marcados (100). Existen 8 productos independientes de términos (97) con (98):
| (101) | |||
| (102) | |||
| (103) | |||
| (104) | |||
| (105) | |||
| (106) | |||
| (107) | |||
| (108) |
Estas son entonces las constantes del movimiento correspondientes a nuestro problema. Son perfectamente aceptables; sin embargo nuestro interés principal consiste en construir, a partir de ellas, el grupo de simetría apropiado ; o sea, queremos hallar, a partir de ellas, los generadores de dicho grupo. Como tal condición de generadores se da en términos de sus relaciones con respecto a paréntesis de Poisson, se calculará ahora la tabla de paréntesis de Poisson de las F's. Usando (91), se demuestra que:
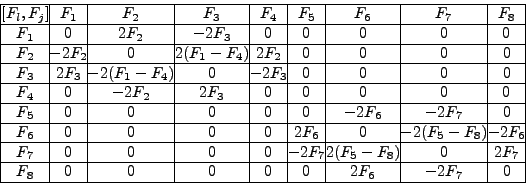
De la tabla 1, se deducen las siguientes constantes del movimiento;
| (109) | |||
| (110) |
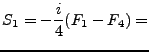 |
|||
| (111) |
 |
|||
| (112) |
 |
|||
| (113) |
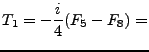 |
|||
| (114) |
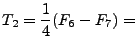 |
|||
| (115) |
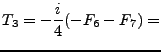 |
|||
| (116) |
Los paréntesis de Poisson de estas constantes del movimiento se dan en la siguiente tabla, en la construcción de la cual se usó la tabla 1;
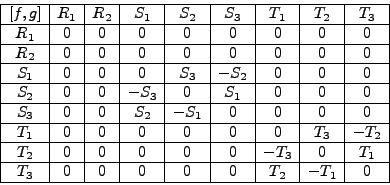
En forma compacta, estas relaciones son las siguientes:
Para
![]() :
:
| (117) | |||
| (118) |
| (119) |
| (120) |
| (121) |
| (122) |
Las anteriores relaciones de conmutación indican [13] que las
constantes del movimiento halladas son generadores del gupo O(4),
o sea se ha demostrado que el grupo de simetría del problema
representado por el Hamiltoniano ![]() (ec. (2)) es O(4).
(ec. (2)) es O(4).
La demostración anterior es perfectamente rigurosa y válida; sin embargo, las constantes del movimiento obtenidos no tienen una interpretación geométrica directa. Lo que se hará ahora es construir, a partir de las constantes del movimiento (109-116), funciones que también sean constantes del movimiento pero que tengan un significado geométrica conocido. Para hacer ésto, nos guiaremos por el tratamiento vectorial que se dió al problema en la sección I-B. En dicho estudio vectorial, se demostró (ecs. (7,23) de la sección I-B) que:
| (123) |
| (124) |
Introduciendo el vector ![]() dado por:
dado por:

Se puede poner a ![]() y
y ![]() en función de las
en función de las
![]() . Sin embargo resulta más fácil trabajar con
las coordenadas y momenta originales
. Sin embargo resulta más fácil trabajar con
las coordenadas y momenta originales
Para realizar lo anterior, se necesitan las ![]() en
función de las coordenadas
en
función de las coordenadas
![]() .
Usando las relaciones (40-43, 48-51), así como la ecuación (80),
se demuestra que;
.
Usando las relaciones (40-43, 48-51), así como la ecuación (80),
se demuestra que;
![$\displaystyle [2(-2mE)^{\frac{1}{2}}]^{-\frac{1}{2}} \left [
(-2mE)^\frac{1}{2}...
...box{cos}\theta \;P_\mu - \mbox{sen}\theta\;
\frac{P_\theta}{\mu}) \right] \cdot$](img521.png) |
|||
![$\displaystyle \left [ e^{\mp(\pi i B^{-\frac{1}{2}})(-2mE)^{\frac{1}{2}}(\mu P _\mu + \nu P_\nu)} \right ]$](img522.png) |
(125) |
![$\displaystyle [2(-2mE)^{\frac{1}{2}}]^{-\frac{1}{2}} \left [
(-2mE)^\frac{1}{2}...
...ox{sen}\theta \;P_\mu + \mbox{cos}\theta\;
\frac{P_\theta}{\mu}) \right ] \cdot$](img524.png) |
|||
![$\displaystyle \left [ e^{\mp(\pi i B^{-\frac{1}{2}})(-2mE)^{\frac{1}{2}}(\mu P _\mu + \nu P_\nu)} \right ]$](img522.png) |
(126) |
Para ![]() y
y ![]() sólo hay que cambiar
sólo hay que cambiar ![]() por
por ![]() por
por ![]() y
y ![]() por
por ![]() en (125) y (126), respectivamente:
en (125) y (126), respectivamente:
![$\displaystyle [2(-2mE)^{\frac{1}{2}}]^{-\frac{1}{2}} \left [
(-2mE)^\frac{1}{2}...
...box{cos}\delta \;P_\nu - \mbox{sen}\delta\;
\frac{P_\delta}{\nu}) \right] \cdot$](img532.png) |
|||
![$\displaystyle \left [ e^{\mp(\pi i B^{-\frac{1}{2}})(-2mE)^{\frac{1}{2}}(\mu P _\mu + \nu P_\nu)} \right ]$](img522.png) |
(127) |
![$\displaystyle [+2(-2mE)^{\frac{1}{2}}]^{-\frac{1}{2}} \left [
(-2mE)^\frac{1}{2...
...ox{sen}\delta \;P_\nu + \mbox{cos}\delta\;
\frac{P_\delta}{\nu}) \right ] \cdot$](img534.png) |
|||
![$\displaystyle \left [ e^{\mp(\pi i B^{-\frac{1}{2}})(-2mE)^{\frac{1}{2}}(\mu P _\mu + \nu P_\nu)} \right ]$](img522.png) |
(128) |
Usando las relaciones (125-128), se pondrán ahora las
![]() en función de las coordenadas
en función de las coordenadas
![]() :
:
![$\displaystyle [2(-2mE)^{\frac{1}{2}}]^{-1} [-2mE\mu^2
\mbox{cos}^2 \theta + \mbox{cos}^2 \theta P_\mu^2 + \mbox{sen}^2
\theta \frac{P^2_\theta}{\mu^2}$](img537.png) |
|||
![$\displaystyle -2 \mbox{sen}\theta \;\mbox{cos}\theta \;\frac{P_\mu P_\theta}{\mu}]$](img538.png) |
(129) |
![$\displaystyle [2(-2mE)^{\frac{1}{2}}]^{-1} [-2mE\mu^2
\mbox{sen}^2 \theta + \mbox{sen}^2 \theta P_\mu^2 + \mbox{cos}^2
\theta \frac{P^2_\theta}{\mu^2}$](img540.png) |
|||
![$\displaystyle +2 \mbox{sen}\theta \;\mbox{cos}\theta \;\frac{P_\mu P_\theta}{\mu}]$](img541.png) |
(130) |
![$\displaystyle [2(-2mE)^{\frac{1}{2}}]^{-1} [-2mE\nu^2
\mbox{cos}^2 \delta + \mbox{cos}^2 \delta P_\nu^2 + \mbox{sen}^2
\delta \frac{P^2_\delta}{\nu^2}$](img543.png) |
|||
![$\displaystyle -2 \mbox{sen}\delta \;\mbox{cos}\delta \;\frac{P_\mu P_\delta}{\nu}]$](img544.png) |
(131) |
![$\displaystyle [2(-2mE)^{\frac{1}{2}}]^{-1} [-2mE\nu^2
\mbox{sen}^2 \delta + \mbox{sen}^2 \delta P_\nu^2 + \mbox{cos}^2
\delta \frac{P^2_\delta}{\nu^2}$](img546.png) |
|||
![$\displaystyle +2 \mbox{sen}\delta \;\mbox{cos}\delta \;\frac{P_\nu P_\delta}{\nu}]$](img547.png) |
(132) |
![$\displaystyle [2(-2mE)^\frac{1}{2}]^{-1} \left \{\mbox{cos}\theta\;\mbox{cos}\d...
...)^\frac{1}{2} \frac{\mu P_\delta}{\nu} + \frac{P_\mu P_\delta}{\nu}] + \right.$](img549.png) |
|||
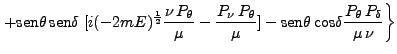 |
(133) |
![$\displaystyle [2(-2mE)^\frac{1}{2}]^{-1} \left \{\mbox{cos}\theta\;\mbox{cos}\d...
...)^\frac{1}{2} \frac{\nu P_\theta}{\mu} + \frac{P_\nu P_\theta}{\mu}] + \right.$](img553.png) |
|||
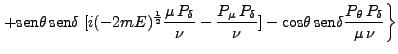 |
(134) |
![$\displaystyle \left. [-2mE\mu^2 + P^2_\mu - \frac{P^2_theta}{\mu^2}] + \frac{P_\mu P_\theta}{\mu} [\mbox{cos}^2 \theta - \mbox{sen}^2 \theta]\right\}$](img558.png) |
(135) |
![$\displaystyle (\mu P_\nu - \nu P_\mu)] + \mbox{cos}\theta \mbox{sen}\delta \; [-i (-2mE)^\frac{1}{2} \frac{\mu P_\delta}{\nu} - \frac{P_\mu P_\delta}{\nu}]$](img561.png) |
|||
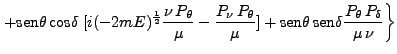 |
(136) |
![$\displaystyle [2 (-2mE)^\frac{1}{2}]^{-1} \left
\{\mbox{sen}\theta \mbox{cos}\theta \; [-2mE\mu^2 + P^2_\mu -
\frac{P^2_\theta}{\mu^2}] \right.$](img564.png) |
|||
![$\displaystyle \left. -i (-2mE)^\frac{1}{2} P_\theta + \frac{P_\mu P_\theta}{\mu}[\mbox{cos}^2 \theta- \mbox{sen}^2\theta]\right\}$](img565.png) |
(137) |
![$\displaystyle (\mu P_\nu - \nu P_\mu)] + \mbox{sen}\theta \mbox{sen}\delta \; [-i (-2mE)^\frac{1}{2} \frac{\mu P_\delta}{\nu} - \frac{P_\mu P_\delta}{\nu}]$](img568.png) |
|||
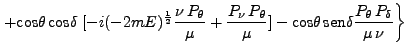 |
(138) |
![$\displaystyle (\mu P_\nu - \nu P_\mu)] + \mbox{sen}\theta \mbox{cos}\delta \; [i (-2mE)^\frac{1}{2} \frac{\mu P_\delta}{\nu} + \frac{P_\mu P_\delta}{\nu}]$](img572.png) |
|||
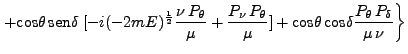 |
(139) |
![$\displaystyle (\mu P_\nu - \nu P_\mu)] + \mbox{cos}\theta \mbox{sen}\delta \; [i (-2mE)^\frac{1}{2} \frac{\mu P_\delta}{\nu} - \frac{P_\mu P_\delta}{\nu}]$](img576.png) |
|||
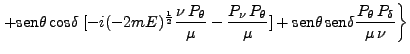 |
(140) |
![$\displaystyle \left. [-2mE \nu^2 + P^2_\nu - \frac{P^2_\delta}{\nu^2}] + \frac{P_\nu P_\delta}{\nu}\;(\mbox{cos}^2\delta - \mbox{sen}^2\delta]\right\}$](img580.png) |
(141) |
![$\displaystyle (\mu P_\nu - \nu P_\mu)] + \mbox{sen}\theta \mbox{sen}\delta \; [-i (-2mE)^\frac{1}{2} \frac{\mu P_\theta}{\mu} - \frac{P_\nu P_\theta}{\mu}]$](img583.png) |
|||
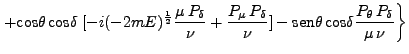 |
(142) |
![$\displaystyle (\mu P_\nu - \nu P_\mu)] + \mbox{sen}\theta \mbox{cos}\delta \; [-i (-2mE)^\frac{1}{2} \frac{\mu P_\delta}{\nu} + \frac{P_\mu P_\delta}{\nu}]$](img587.png) |
|||
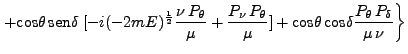 |
(143) |
![$\displaystyle [2(-2mE)^\frac{1}{2}]^{-1}
\left\{\mbox{sen}\delta\;\mbox{cos}\delta \; [-2mE\nu^2 + P^2_\nu
- \frac{P^2_\delta}{\nu^2}] \right.$](img589.png) |
|||
![$\displaystyle \left. -i (-2mE)^\frac{1}{2} P_\delta + \frac{P_\nu P_\delta}{\nu} [\mbox{cos}^2 \delta - \mbox{sen}^2\delta]\right\}$](img590.png) |
(144) |
Usando las relaciones (109-116) y (129-144), es posible escribir las
constantes del movimiento
![]() en función de
en función de
![]() obteniéndose las relaciones siguientes:
obteniéndose las relaciones siguientes:
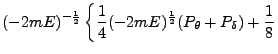 |
|||
![$\displaystyle \left. [-2mE (\mu^2 - \nu^2) +
P^2_\mu - P^2_\nu + \frac{P^2_\theta}{\mu^2} -
\frac{P^2_\delta}{\nu^2}]\right\}$](img595.png) |
(145) |
 |
|||
![$\displaystyle -2mE\mu \nu + P_\mu P_\nu - \frac{P_\theta P_\delta}{\mu \nu}] + \frac{1}{4} [\mbox{sen}(\theta + \delta)]$](img598.png) |
|||
![$\displaystyle \left. [-(-2mE)^{\frac{1}{2}} (\mu P_\nu - \nu P_\mu) - \frac{P_\mu P_\delta}{\nu} - \frac{P_\nu P_\theta}{\mu}]\right\}$](img599.png) |
(146) |
 |
|||
![$\displaystyle \frac{P_\mu P_\delta}{\nu} + \frac{P_\nu P_\theta}{\mu}] + \fra...
...) [(-2mE)^{\frac{1}{2}} (\frac{\nu P_\theta}{\mu} - \frac{\mu P_\delta}{\nu})$](img602.png) |
|||
![$\displaystyle \left. -2mE \mu \nu + P_\mu P_\nu - \frac{P_\theta P_\delta}{\mu \nu}]\right\}$](img603.png) |
(147) |
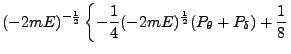 |
|||
![$\displaystyle \left. [-2mE (\mu^2 - \nu^2) +
P^2_\mu - P^2_\nu + \frac{P^2_\theta}{\mu^2} -
\frac{P^2_\delta}{\nu^2}]\right\}$](img595.png) |
(148) |
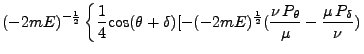 |
|||
![$\displaystyle -2mE\mu \nu + P_\mu P_\nu - \frac{P_\theta P_\delta}{\mu \nu}] + \frac{1}{4} \mbox{sen}(\theta + \delta)$](img608.png) |
|||
![$\displaystyle \left. [(-2mE)^{\frac{1}{2}} (\mu P_\nu - \nu P_\mu) - \frac{P_\mu P_\delta}{\nu} - \frac{P_\nu P_\theta}{\mu}]\right\}$](img609.png) |
(149) |
 |
|||
![$\displaystyle \frac{P_\mu P_\delta}{\nu} - \frac{P_\nu P_\theta}{\mu}] + \fra...
...) [(-2mE)^{\frac{1}{2}} (\frac{\nu P_\theta}{\mu} - \frac{\mu P_\delta}{\nu})$](img612.png) |
|||
![$\displaystyle \left. +2mE \mu \nu - P_\mu P_\nu + \frac{P_\theta P_\delta}{\mu \nu}]\right\}$](img613.png) |
(150) |
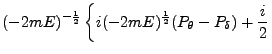 |
|||
![$\displaystyle \left. [-2mE(\mu^2 + \nu^2) + P_\mu^2 + P_\nu^2 + \frac{P_\theta^2}{\mu^2} + \frac{P_\delta^2}{\nu^2}]\right\}$](img616.png) |
(151) |
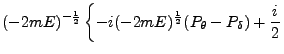 |
|||
![$\displaystyle \left. [-2mE(\mu^2 + \nu^2) + P_\mu^2 + P_\nu^2 + \frac{P_\theta^2}{\mu^2} + \frac{P_\delta^2}{\nu^2}]\right\}$](img616.png) |
(152) |
Se pondrán ahora
![]() y
y ![]() en función de
en función de
![]() . Para esto, según es
evidente de sus definiciones, se necesita a
. Para esto, según es
evidente de sus definiciones, se necesita a ![]() y
y
![]() en función de estas coordenadas.
en función de estas coordenadas.
De sus definiciones (ecs. (124 a-b)):
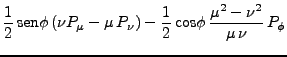 |
(153) | ||
 |
(154) | ||
| (155) |
| (156) | |||
| (157) | |||
| (158) |
Entonces, usando las relaciones 153-158, 12-14, 3-8, 123-a,34-37,124), se tiene que:
 |
|||
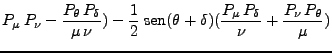 |
(159) |
 |
|||
![$\displaystyle \frac{1}{2} \;\mbox{sen}(\theta + \delta) [-(-2mE \mu \nu + P_\mu P_\nu - \frac{P_\theta P_\delta}{\mu \nu})]$](img639.png) |
(160) |
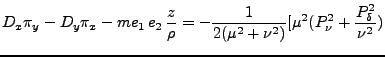 |
|||
![$\displaystyle - \nu^2(P^2_\mu + \frac{P^2_\theta}{\mu^2}) + 2me_1 e_2 (\mu^2 - \nu^2)]$](img642.png) |
(161) |
En lo anterior, se ha usado la relación (34) para poner
![]() en el lugar de
en el lugar de ![]() . Para el vector
. Para el vector ![]() :
:
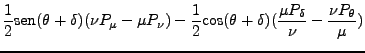 |
(162) | ||
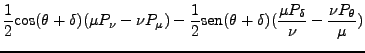 |
(163) | ||
 |
(164) |
De las relaciones (145-150) y (159-164) se tiene casi directamente
(sólo hay que hacer algunas transformaciones algebraicas usando
(38)
para ![]() ):
):
| (165) |
| (166) |
| (167) |
| (168) |
| (169) |
| (170) |
Definiendo un nuevo vector
![]() por:
por:
| (171) |
| (172) |
| (173) |
| (174) |
De las relaciones (117-122, 168-170, 172-174), es directo demostrar, usando la propiedad de antisimetría de los paréntesis de Poisson con respecto a un cambio de orden en sus argumentos, las siguientes relaciones:
| (175) |
| (176) |
| (177) |
Estas relaciones indican [13] que
![]() son generadores del grupo
son generadores del grupo ![]() . Con ésto, se ha conseguido lo
que se quería: dar a las constantes del movimiento una
interpretación geométrica y tener así generadores del
grupo
. Con ésto, se ha conseguido lo
que se quería: dar a las constantes del movimiento una
interpretación geométrica y tener así generadores del
grupo ![]() más convencionales que
más convencionales que
![]() .
.