



Next: Sobreyectividad
Up: Ancestros
Previous: Ancestros
Contents
Sea
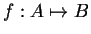 una función donde los
elementos del conjunto B son todas las configuraciones posibles
para un autómata dado y los elementos del conjunto
una función donde los
elementos del conjunto B son todas las configuraciones posibles
para un autómata dado y los elementos del conjunto 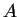 son todos
los ancestros que tienen dichas configuraciones. Se dice que
son todos
los ancestros que tienen dichas configuraciones. Se dice que 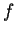 es una función
es una función 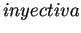 si y solo si se satisface la
siguiente propiedad: si
si y solo si se satisface la
siguiente propiedad: si
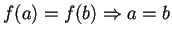 , es decir,
cuando los elementos que componen la imagen están relacionados
con uno y solo un elemento del dominio, tal como se muestra en la
figura 3.20.
, es decir,
cuando los elementos que componen la imagen están relacionados
con uno y solo un elemento del dominio, tal como se muestra en la
figura 3.20.
Figura 3.20:
Función inyectiva.
|
|
Se puede observar en la figura 3.20 que existen elementos que no
forman parte de la función, es decir, en el conjunto B hay
elementos que no están relacionados con ningún elemento del
conjunto A.
Los elementos que no forman parte del
conjunto imagen representan configuraciones que no pueden ser
generadas a partir de otras configuraciones. Dadas sus
características, a estos elementos se les identifica con el
término Jardín del Edén.
Por lo antes
mencionado, un Jardín del Edén solo podrá ser una
configuración inicial la cual no aparecerá de nuevo durante la
evolución del autómata.
Las condiciones que
determinan el surgimiento de este fenómeno son bastante
complejas. Existen artículos tales como los de S. Amoroso y
G. Cooper [1], Moore [53], McIntosh [50]
y Sven Skyum [90] donde se determina de manera rigurosa y
formal el surgimiento de Jardines del Edén.




Next: Sobreyectividad
Up: Ancestros
Previous: Ancestros
Contents
rene
2003-10-20
![\includegraphics[width=3in]{3-20r}](img122.gif)