Sobreyectividad

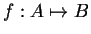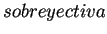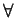
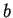
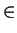
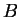
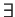
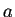
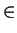
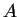
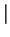
Se dice que $f: A \mapsto B$ es una función $sobreyectiva$ si y solo si se satisface la siguiente propiedad: 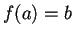$\forall$ $b$ $\in$ $B$ $\exists$ $a$ $\in$ $A$ $\mid$ $f(a) = b$, es decir, una función es sobreyectiva si el codominio de la función coincide con la imagen de la misma, tal como se muestra en la figura 3.21.

Figura 3.21: Función sobreyectiva.

El hecho de que en una función sobreyectiva la imagen tiene que coincidir con el codominio es un indicativo de que cualquier configuración generada durante la evolución del autómata (incluyendo la configuración inicial) tendrá por lo menos un ancestro; esto hace desaparecer la posibilidad de que existan Jardines del Edén. Por otra parte, en la figura 3.21 se aprecia que existen elementos en el conjunto imagen B que están relacionados con más de un elemento del conjunto A, esto quiere decir que existen configuraciones que pueden ser generadas a partir de varias configuraciones diferentes, en otras palabras, una configuración puede tener múltiples ancestros.