Biyectividad

Una función 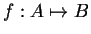$f: A \mapsto B$ es biyectiva si es inyectiva y es sobreyectiva a la vez, es decir, todos los elementos del conjunto B (sobreyectividad) tienen que estar relacionados con uno y solo un elemento del conjunto A (inyectividad). Cuando hay biyectividad no existen ni Jardines del Edén ni ancestros múltiples, por lo tanto, todas las configuraciones generadas tienen ancestros únicos, o dicho de otra manera, el autómata es reversible, es decir, se puede encontrar una regla que reproduzca las evoluciones del autómata de forma inversa.

Un claro ejemplo de biyectividad se puede observar en el ciclo generado por un autómata (2,1) aplicando la regla 54 presentado en la figura 3.19. En la figura 3.22 se ilustra este mismo ciclo en forma de conjuntos.

Figura 3.22: Función biyectiva.