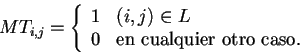Next: Diagrama de Bruijn
Up: Teoría de autómata celular
Previous: Biyectividad
Contents
La teoría de gráficas juega un rol importante
en la teoría de autómata celular, según afirma McIntosh
en [51], ya que por medio de ésta es posible describir
la evolución del autómata y relacionar sus propiedades locales
con sus propiedades globales.
Desde un punto de
vista puramente abstracto, una gráfica consta de 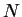 nodos y de
nodos y de
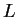 ligas. Los nodos son un conjunto formado a menudo por enteros
no negativos desde
ligas. Los nodos son un conjunto formado a menudo por enteros
no negativos desde 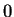 hasta
hasta 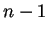 , mientras que las ligas son
un conjunto formado del producto cartesiano
, mientras que las ligas son
un conjunto formado del producto cartesiano 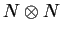 .
.
Para trazar una gráfica, simplemente se dibujan los
nodos, los cuales son frecuentemente etiquetados de acuerdo a los
elementos del conjunto 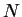 , y las ligas, las cuales son
representadas por flechas juntando a los nodos. Una liga va desde
el nodo
, y las ligas, las cuales son
representadas por flechas juntando a los nodos. Una liga va desde
el nodo 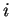 hasta el nodo
hasta el nodo 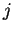 si
si 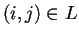 .
.
La
ecuación que define a la matriz topológica de una gráfica es
la siguiente:
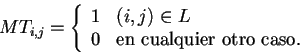 |
(3.1) |
Un punto importante a destacar acerca de la matriz
topológica es el hecho de que los e-lementos que la conforman
describen las rutas entre los nodos, los cuales a su vez,
contienen múltiples ligas, de acuerdo al elemento involucrado.
Debido a que los elementos de la matriz topológica son enteros,
éstos son útiles para contar el número total de rutas.
Aquí hay que hacer notar que las rutas no están bajo
ningún criterio de clasificación.
La idea
fundamental de lo que es una gráfica es un punto de partida para
crear he-rramientas las cuales pueden ser empleadas para ciertos
fines específicos. Un ejemplo de esto son los diagramas de
Bruijn3.3, herramienta principal de la teoría de
registro de corri-mientos. La teoría de registro de
corrimientos es una disciplina basada en el tratamiento de
secuencias superponiéndose; debido a que en un autómata
celular lineal las vecindades se van superponiendo no es
difícil imaginar que los diagramas de Bruijn y sus
subdiagramas (de subconjuntos) puedan ser útiles en el
análisis de los autómatas celulares en una dimensión.
Subsections




Next: Diagrama de Bruijn
Up: Teoría de autómata celular
Previous: Biyectividad
Contents
rene
2003-10-20