



Next: Diagrama de subconjuntos
Up: Herramientas gráficas para el
Previous: Herramientas gráficas para el
Contents
Los nodos del diagrama de Bruijn son secuencias de
símbolos de algún alfabeto, justo como en las expresiones
regulares. Las ligas del diagrama describen la manera en la cual
tales secuencias pueden superponerse. Diferentes grados de
superposición llevan a diferentes diagramas. En el diagrama
básico, la superposición consta de un símbolo inicial, un
símbolo que relaciona las secuencias y un símbolo
terminal.
Cuando los símbolos que representan los estados del autómata celular son enteros, la
faci-lidad de tratar sus propiedades aritméticamente o
algebráicamente motiva a la utilización de esta herramienta.
Por ejemplo, la ecuación que define a la matriz topológica de
un diagrama de Bruijn es:
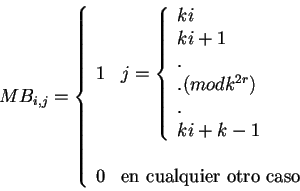 |
(3.2) |
donde 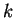 representa el número de estados y
representa el número de estados y 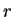 el radio de
vecindad. La variable
el radio de
vecindad. La variable 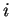 , la cual representa el renglón de la
matriz va a tomar valores desde
, la cual representa el renglón de la
matriz va a tomar valores desde 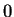 hasta
hasta  , mientras
que la variable
, mientras
que la variable 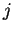 , la cual representa la columna de la matriz
tomará valores de acuerdo a los valores que tengan
, la cual representa la columna de la matriz
tomará valores de acuerdo a los valores que tengan 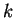 ,
, 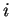 y
y
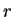 (para algunos casos). Así pues, para un autómata celular
lineal (2,1) los valores de
(para algunos casos). Así pues, para un autómata celular
lineal (2,1) los valores de 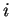 y de
y de 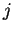 se generan de la
siguiente manera: si
se generan de la
siguiente manera: si 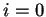 entonces
entonces 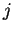 va a tomar valores a
partir de las operaciones
va a tomar valores a
partir de las operaciones 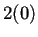 y
y 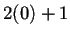 , por lo tanto en este
caso
, por lo tanto en este
caso 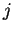 toma los valores
toma los valores 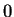 y
y 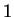 respectivamente. Si
respectivamente. Si 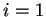 entonces
entonces 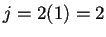 y
y 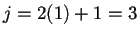 . Si
. Si 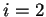 entonces
entonces 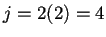 módulo
módulo 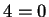 y
y 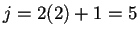 módulo
módulo 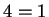 . Si
. Si 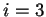 entonces
entonces
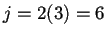 módulo
módulo 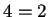 y
y 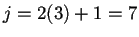 módulo
módulo 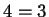 . La matriz
topológica de Bruijn MB que se obtiene a partir de la ecuación
3.2 es la siguiente:
. La matriz
topológica de Bruijn MB que se obtiene a partir de la ecuación
3.2 es la siguiente:
Cabe mencionar que los valores de 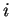 van de
van de 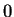 a
a 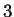 debido a que la cardinalidad del conjunto
debido a que la cardinalidad del conjunto 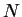 (la cual está
determinada por
(la cual está
determinada por 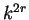 ) es
) es 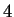 puesto que
puesto que 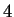 nodos pueden
representar todas las vecindades posibles de tres células para
un autómata celular lineal (2,1). En la figura 3.23 se observan
estas vecindades, las cuales se obtienen de la siguiente forma:
consideremos el nodo con la etiqueta
nodos pueden
representar todas las vecindades posibles de tres células para
un autómata celular lineal (2,1). En la figura 3.23 se observan
estas vecindades, las cuales se obtienen de la siguiente forma:
consideremos el nodo con la etiqueta 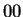 y el nodo con la
etiqueta
y el nodo con la
etiqueta 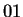 ; para que exista una liga entre ambos, debe
coincidir el último símbolo del nodo que se considera de
partida con el primer símbolo del nodo que se considera de
llegada. En este caso si tomamos el nodo
; para que exista una liga entre ambos, debe
coincidir el último símbolo del nodo que se considera de
partida con el primer símbolo del nodo que se considera de
llegada. En este caso si tomamos el nodo 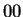 como nodo de partida
y el nodo
como nodo de partida
y el nodo 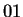 como nodo de llegada, podremos verificar que el
símbolo
como nodo de llegada, podremos verificar que el
símbolo 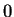 enlaza a los dos nodos y por lo tanto puede
existir una liga que conecte al nodo
enlaza a los dos nodos y por lo tanto puede
existir una liga que conecte al nodo 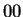 con el nodo
con el nodo 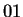 . En el
caso contrario, es decir, si se toma el nodo
. En el
caso contrario, es decir, si se toma el nodo 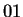 como nodo de
partida y el nodo
como nodo de
partida y el nodo 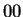 como nodo de llegada, no podrá existir
una liga de enlace entre ambos nodos puesto que el último
símbolo del nodo de partida no coincide con el primer
síimbolo del nodo de llegada. Esta misma verificación se
realiza para todos los nodos del diagrama para establecer todas
las ligas posibles. Cabe mencionar que las etiquetas de los nodos
del diagrama de Bruijn genérico para un autómata celular
lineal (2,1) son símbolos que forman vecindades
parciales. Para el caso genérico, las vecindades parciales de
dos células forman una vecindad completa de tres células al
superponer el símbolo que establece la liga entre dos nodos.
En todo diagrama de Bruijn los nodos están etiquetados con
vecindades parciales las cuales están conformadas por un
número par de células. En el siguiente capítulo
analizaremos diagramas de Bruijn con vecindades parciales de más
de dos células.
como nodo de llegada, no podrá existir
una liga de enlace entre ambos nodos puesto que el último
símbolo del nodo de partida no coincide con el primer
síimbolo del nodo de llegada. Esta misma verificación se
realiza para todos los nodos del diagrama para establecer todas
las ligas posibles. Cabe mencionar que las etiquetas de los nodos
del diagrama de Bruijn genérico para un autómata celular
lineal (2,1) son símbolos que forman vecindades
parciales. Para el caso genérico, las vecindades parciales de
dos células forman una vecindad completa de tres células al
superponer el símbolo que establece la liga entre dos nodos.
En todo diagrama de Bruijn los nodos están etiquetados con
vecindades parciales las cuales están conformadas por un
número par de células. En el siguiente capítulo
analizaremos diagramas de Bruijn con vecindades parciales de más
de dos células.
Figura 3.23:
Diagramas de Bruijn genéricos para un autómata
celular lineal (2,1). En el diagrama del lado izquierda (a) las
vecindades parciales están expresadas en notación binaria,
mientras que en el diagrama del lado derecho (b) están en
notación decimal.
|
|
En la figura 3.24 se muestra el diagrama de Bruijn de la regla 54.
En ésta se ilustran las ligas que producen cada una de las ocho
vecindades y se resaltan con color negro aquellas en las cuales
sus respectivas células centrales evolucionan al estado 1.
Figura 3.24:
Diagrama de Bruijn de la regla 54.
|
|




Next: Diagrama de subconjuntos
Up: Herramientas gráficas para el
Previous: Herramientas gráficas para el
Contents
rene
2003-10-20
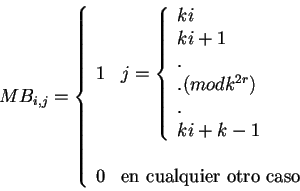
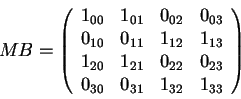
![\includegraphics[width=4.2in]{3-23r}](img160.gif)