



Next: Modelo de Fuks y
Up: Analizando la regla de
Previous: Analizando la regla de
Contents
El modelo que representa el tránsito de
automóviles con la dinámica más simple es aquel en el
cual los autos se desplazan de izquierda a derecha de manera
sincronizada en cada paso de tiempo a través de un solo carril
por la carretera, misma que se representa por un conjunto de
celdas las cuales pueden estar desocupadas u ocupadas por un
vehículo
(ver figura 4.1).
Figura 4.1:
Carril de una carretera representada por medio de
celdas.
|
|
En este modelo, las velocidades de los autos se representan
mediante la variable 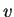 , la cual puede tener sólo dos valores:
0 y 1. Cuando
, la cual puede tener sólo dos valores:
0 y 1. Cuando 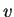 es igual a 0 significa que el auto está
detenido, y cuando
es igual a 0 significa que el auto está
detenido, y cuando 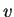 es igual a 1 significa que el auto puede
avanzar un espacio hacia adelante. Como podemos notar, los valores
que puede asumir
es igual a 1 significa que el auto puede
avanzar un espacio hacia adelante. Como podemos notar, los valores
que puede asumir 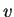 nos indican que los autos sólo pueden
alcanzar una velocidad igual a 1, mismo número de sitios que los
vehículos pueden avanzar como máximo. De esta manera, la
velocidad máxima que pueden alcanzar los autos, la cual es
representada mediante el parámetro
nos indican que los autos sólo pueden
alcanzar una velocidad igual a 1, mismo número de sitios que los
vehículos pueden avanzar como máximo. De esta manera, la
velocidad máxima que pueden alcanzar los autos, la cual es
representada mediante el parámetro 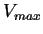 es igual a 1 y el promedio de
velocidad es dado por
es igual a 1 y el promedio de
velocidad es dado por
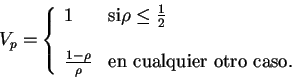 |
(4.1) |
donde 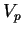 es el promedio de velocidad que mantienen los autos después de un número determinado de iteraciones. El valor de
es el promedio de velocidad que mantienen los autos después de un número determinado de iteraciones. El valor de 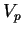 es determinado por la densidad
es determinado por la densidad 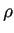 la cual se representa por el número de autos en la carretera. En la figura 4.2 se ilustra como varía
la cual se representa por el número de autos en la carretera. En la figura 4.2 se ilustra como varía 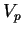 de acuerdo a
de acuerdo a 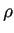 .
.
Se encontró una equivalencia entre la mecánica de este
modelo y la regla de AC(2,1) 184 estudiada por Wolfram
[101] la cual se muestra en la tabla 4.1.
Tabla 4.1:
Regla de AC(2,1) 184.
| Vecindad |
Estado al que evoluciona la célula central |
| 000 |
0 |
| 001 |
0 |
| 010 |
0 |
| 011 |
1 |
| 100 |
1 |
| 101 |
1 |
| 110 |
0 |
| 111 |
1 |
|
Figura 4.2:
Promedio de velocidad de los autos en función de la densidad.
|
|
Figura 4.3:
(a) Desplazamiento de los autos aplicando el modelo que
incluye los parámetros 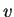 y
y 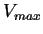 . (b) Desplazamiento de
los autos aplicando la regla de evolución 184 para un AC(2,1).
. (b) Desplazamiento de
los autos aplicando la regla de evolución 184 para un AC(2,1).
|
|
En el caso de la regla 184, las células que están en
estado 0 representan un sitio vacío (no un sitio ocupado por
un auto con velocidad 0), mientras que las que están en estado 1
representan un sitio ocupado por un auto (no un sitio ocupado por
un auto con velocidad 1). Al observar esta regla no hay que tomar
en cuenta velocidades, solamente hay que observar que los sitios
vacíos se representan con el estado 0 y los sitios ocupados con el
estado 1. Haciendo evolucionar este autómata se puede comprobar
que los 1's se desplazan de izquierda a derecha en cada
generación siempre y cuando haya ceros a su derecha.
Aunque la
dinámica de la regla 184 no toma en cuenta las
velocidades, su patrón de comportamiento es equivalente al del
modelo que incluye a 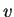 y
y 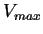 cuando
cuando 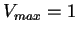 .
Esto se puede apreciar en la figura 4.3 en la cual se ilustra como
se desplazan los autos aplicando la regla 184 y el modelo que
incluye a
.
Esto se puede apreciar en la figura 4.3 en la cual se ilustra como
se desplazan los autos aplicando la regla 184 y el modelo que
incluye a 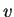 y
y 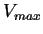 .
.
Se han creado otros
modelos a partir de la regla 184, con la variante de que los autos se desplazan
en bloque, con esto lo que se busca es aumentar la fluidez sin modificar el número de velocidades diferentes a las que se pueden desplazar los
automóviles.
Han surgido modelos como el ``tránsito monitoreado" de Fuks y Boccara
[24] y una generalización del modelo de Takayasu y
Takayasu [91], los cuales se explican en las
siguientes secciones.




Next: Modelo de Fuks y
Up: Analizando la regla de
Previous: Analizando la regla de
Contents
rene
2003-10-20
![\includegraphics[width=4in]{4-1r}](img167.gif)
![\includegraphics[width=3in]{4-3r}](img170.gif)
![]() y
y ![]() cuando
cuando ![]() .
Esto se puede apreciar en la figura 4.3 en la cual se ilustra como
se desplazan los autos aplicando la regla 184 y el modelo que
incluye a
.
Esto se puede apreciar en la figura 4.3 en la cual se ilustra como
se desplazan los autos aplicando la regla 184 y el modelo que
incluye a ![]() y
y ![]() .
.