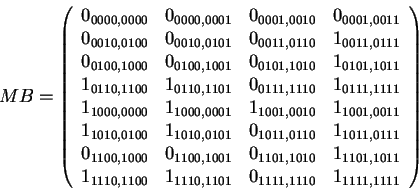Next: Comentarios
Up: Analizando la regla de
Previous: Modelo de arranque lento
Contents
En el capítulo anterior explicamos la forma de
construir un diagrama de Bruijn. En el diagrama de Bruijn está
contenida toda la información referente al comportamiento y a
las características propias del autómata celular. En la
figura 4.8 se muestra el diagrama de Bruijn básico de la regla
184.
Figura 4.8:
Diagrama de Bruijn de la regla 184.
|
|
A partir del diagrama básico se pueden obtener, por ejemplo, las
configuraciones still lifes las cuales se observan en el
subdiagrama de la figura 4.9. Como se puede apreciar, solamente se
conservan las ligas que representan las vecindades cuya célula
central se conserva después de aplicar la regla de evolución.
En este subdiagrama existen dos ciclos que llevan a secuencias
infinitas de 0's y 1's, las cuales son las configuraciones
still lifes.
Figura 4.9:
Subdiagrama que muestra las configuraciones still
lifes de la regla 184.
|
|
Sin embargo, es difícil identificar mucha información a
partir del diagrama básico de un autómata. Por esta razón es
útil analizar subdiagramas derivados del diagrama de Bruijn de
un autómata celular específico como son los diagramas de
subconjuntos y de ciclos. Además, el mismo diagrama de Bruijn se
puede ampliar utilizando nodos con vecindades parciales de
tamaño más grande que las mínimas necesarias para
construir el diagrama básico. Cabe mencionar que las vecindades
parciales deben ser de tamaño par puesto que las vecindades
completas que resultan de conectar dos nodos deben ser de tamaño
impar.
En la figura 4.10 se muestra el diagrama de
subconjuntos de la regla 184. En este diagrama se puede apreciar
una ruta que va del nodo etiquetado con el número 15 al nodo
etiquetado con el símbolo que representa al conjunto
vacío, es decir, del nodo máximo al nodo mínimo, lo cual
significa que existen configuraciones del tipo Jardín
del Edén. En este caso la secuencia 1100 y todas sus
subsecuencias no podrán ser producidas a partir de otras
configuraciones, con lo que se comprueba que la regla 184 tiene
características de inyectividad.
Figura 4.10:
Diagrama de subconjuntos de la regla 184. Las ligas de
color negro representan subconjuntos que se conectan con otros
subconjuntos a través del estado 1, mientras que las ligas de
color gris representan lo mismo pero a través del estado 0.
|
|
El propósito de utilizar diagramas de Bruijn extendidos es el de
poder examinar a detalle el comportamiento del autómata más
allá de una generación.
Tabla 4.2:
Vecindades de tamaño 5 del diagrama de Bruijn extendido
de la regla 184.
| Nodos conectados |
Generación 0 |
Generación 1 |
Generación 2 |
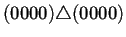 |
00000 |
000 |
0 |
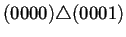 |
00001 |
000 |
0 |
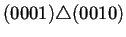 |
00010 |
000 |
0 |
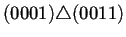 |
00011 |
001 |
0 |
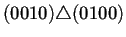 |
00100 |
001 |
0 |
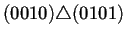 |
00101 |
001 |
0 |
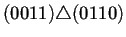 |
00110 |
010 |
0 |
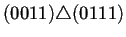 |
00111 |
011 |
1 |
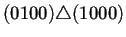 |
01000 |
010 |
0 |
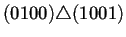 |
01001 |
010 |
0 |
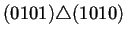 |
01010 |
010 |
0 |
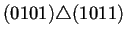 |
01011 |
011 |
1 |
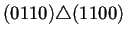 |
01100 |
101 |
1 |
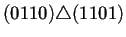 |
01101 |
101 |
1 |
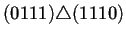 |
01110 |
110 |
0 |
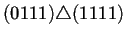 |
01111 |
111 |
1 |
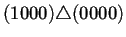 |
10000 |
100 |
1 |
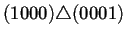 |
10001 |
100 |
1 |
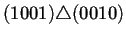 |
10010 |
100 |
1 |
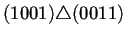 |
10011 |
101 |
1 |
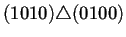 |
10100 |
101 |
1 |
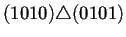 |
10101 |
101 |
1 |
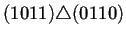 |
10110 |
110 |
0 |
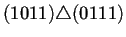 |
10111 |
111 |
1 |
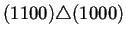 |
11000 |
100 |
1 |
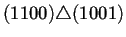 |
11001 |
010 |
0 |
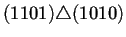 |
11010 |
010 |
0 |
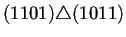 |
11011 |
011 |
1 |
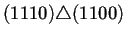 |
11100 |
101 |
1 |
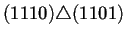 |
11101 |
101 |
1 |
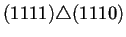 |
11110 |
110 |
0 |
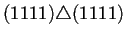 |
11111 |
111 |
1 |
|
Para ilustrar lo anterior la tabla 4.2
muestra la estructura del diagrama de Bruijn extendido a 2
generaciones de la regla de AC(2,1) 184. En la primer columna de
izquierda a derecha se puede observar la forma en que están
conectados los nodos a través del operador de superposición
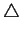 . Para que dos nodos puedan estar conectados se sigue
la misma norma explicada en el capítulo anterior, es decir,
los elementos intermedios de las vecindades parciales que
constituyen los nodos fuente y destino deben coincidir para
conformar junto con las células inicial y final de los nodos
origen y destino respectivamente la vecindad completa, en este
caso, de tamaño 5. Estas vecindades, las cuales constituyen la
generación 0 y se observan en la segunda columna de la tabla 4.2
evolucionan a un solo estado en la segunda generación. Para
obtener esto se toma la primer célula de izquierda a derecha y
las células restantes que completan la vecindad. En este caso,
como se está trabajando con un autómata (2,1) se toman las dos
células de la derecha. Aquí es importante señalar que no
se toman los vecinos de la izquierda porque en la evolución de
las secuencias de un diagrama de Bruijn extendido no se toman en
cuenta los límites periódicos. Una vez que se tiene la
vecindad se aplica la regla de evolución y se obtiene la primera
célula de la siguiente generación, posteriormente se toma la
segunda célula de izquierda a derecha y se repite el proceso
hasta completar la secuencia que constituirá la siguiente
generación.
. Para que dos nodos puedan estar conectados se sigue
la misma norma explicada en el capítulo anterior, es decir,
los elementos intermedios de las vecindades parciales que
constituyen los nodos fuente y destino deben coincidir para
conformar junto con las células inicial y final de los nodos
origen y destino respectivamente la vecindad completa, en este
caso, de tamaño 5. Estas vecindades, las cuales constituyen la
generación 0 y se observan en la segunda columna de la tabla 4.2
evolucionan a un solo estado en la segunda generación. Para
obtener esto se toma la primer célula de izquierda a derecha y
las células restantes que completan la vecindad. En este caso,
como se está trabajando con un autómata (2,1) se toman las dos
células de la derecha. Aquí es importante señalar que no
se toman los vecinos de la izquierda porque en la evolución de
las secuencias de un diagrama de Bruijn extendido no se toman en
cuenta los límites periódicos. Una vez que se tiene la
vecindad se aplica la regla de evolución y se obtiene la primera
célula de la siguiente generación, posteriormente se toma la
segunda célula de izquierda a derecha y se repite el proceso
hasta completar la secuencia que constituirá la siguiente
generación.
Figura 4.11:
Diagrama de Bruijn extendido a vecindades parciales de 4
células.
|
|
Es importante mencionar que si las vecindades que
constituyen las generaciones en la evolución del autómata
fuesen de tamaño par, entonces la evolución no sería
correcta porque las vecindades estarían incompletas. Para
ejemplificar lo anterior tomemos la secuencia 00101 de la
generación 0 de la tabla 4.2. Como se mencionó anteriormente
se toma la primer célula que en este caso es el 0 y las dos
células de la derecha que son 0 y 1 las cuales forman la
vecindad 001. Se aplica la regla de evolución y se obtiene la
primera célula de la siguiente generación la cual es 0. Se
repite el proceso hasta obtener la secuencia 001 que será la
generación 1 y posteriormente se aplica nuevamente la regla de
evolución para obtener un 0. Por lo tanto la secuencia 00101
evoluciona al estado 0 en la segunda generación. El estado 0
será la etiqueta de la liga que une a los dos nodos que forman
la vecindad 00101, estos nodos son el 0010 y el 0101 ó 2 y 5 en
notación decimal. En la figura 4.11 se muestra el diagrama de
Bruijn extendido construido a partir de la tabla 4.2, mientras que
en la figura 4.12 se muestra el diagrama de Bruijn extendido
utilizando vecindades parciales de 6 células.
Figura 4.12:
Diagrama de Bruijn extendido a vecindades parciales de 6
células.
|
|
El número de nodos en un diagrama de Bruijn extendido, al igual que en el
diagrama básico, es dado por 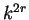 y el número de artistas
por
y el número de artistas
por 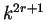 . En el caso del diagrama que utiliza vecindades
parciales de 4 células el número de nodos que contiene el
diagrama aumenta debido a que el tamaño de las vecindades que se
forman al realizar la operación de superposición es 5 y el
radio de vecindad se extiende a 2 vecinos de cada lado. Por lo
tanto, el número de nodos es
. En el caso del diagrama que utiliza vecindades
parciales de 4 células el número de nodos que contiene el
diagrama aumenta debido a que el tamaño de las vecindades que se
forman al realizar la operación de superposición es 5 y el
radio de vecindad se extiende a 2 vecinos de cada lado. Por lo
tanto, el número de nodos es 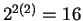 y el número de
artistas es
y el número de
artistas es
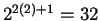 . Lo anterior se aplica para
determinar el número de nodos y de aristas de cualquier diagrama
de Bruijn extendido. Luego, la matriz de conectividad del diagrama de la
figura 4.11 se define de la siguiente manera:
. Lo anterior se aplica para
determinar el número de nodos y de aristas de cualquier diagrama
de Bruijn extendido. Luego, la matriz de conectividad del diagrama de la
figura 4.11 se define de la siguiente manera:
A través de los diagramas de Bruijn extendidos podemos
encontrar los desplazamientos que tendrán ciertas secuencias
durante la evolución del autómata. Estas secuencias se
obtienen a partir de la indentificación de los ciclos en los
diagramas de Bruijn y de tomar como elementos de la secuencia a
analizar los estados que etiquetan a las ligas que conectan a los
nodos que forman el ciclo. Para ejemplificar lo anterior tomemos la secuencia 001 formada de
la siguiente manera: el nodo 0010 se conecta con el nodo 0100, y a
su vez éste se conecta con el nodo 1001 y finalmente se cierra
el ciclo al conectarse éste último con el nodo 0010 y se forma
un pequeño diagrama4.1 que define un acarreo. Si llenamos el espacio que
correspondería a la configuración inicial del autómata celular con la
secuencia 001 (o cualquier permutación de la misma) podremos comprobar que al
aplicar la regla de evolución (tomando ya en cuenta las condiciones de
límites periódicos) las células se desplazan 2 posiciones
a la izquierda en una generación durante la evolución del
autómata.
En este trabajo se encontraron diversos ciclos dentro
de los diagramas de Bruijn extendidos que generan diferentes secuencias; el
propósito de analizar estas secuencias no es el de aportar datos directamente
a la construcción de un diagrama como el de la figura 4.6. De hecho lo que se
pretende es aportar información para poder predecir como se comportarán
ciertas secuencias o ciertas configuraciones con diferentes densidades de autos
a través del tiempo, esto con el fin de complementar los estudios que se
basan en el enfoque de construir diagramas fundamentales y establecer
ecuaciones a partir de los resultados que se obtienen de experimentaciones con
diferentes modelos y variables que estos contienen (densidad, velocidad, etc.).
En la figura 4.13 se muestran los subdiagramas contenidos en los
diagramas de Bruijn extendidos los cuales muestran las diferentes secuencias
con diversos desplazamientos en 1,2 y 3 generaciones aplicando la regla de
AC(2,1) 184.
Como se puede observar en la figura 4.13, existen
acarreos tanto a la izquierda como a la derecha para diferentes densidades de
1's (autos). Los desplazamientos a la izquierda nos pueden servir, por ejemplo,
para determinar de que manera se comportarán los bloques de autómoviles en
cuanto a su desplazamiento a través del tiempo.
Por otra parte,
los desplazamientos a la derecha nos pueden servir para predecir el avance de
ciertas configuraciones de autos sobre la carretera.
Otro tipo de
diagrama que también se obtiene a partir del diagrama de Bruijn y que
también nos sirve para analizar a los autómatas celulares que representan
el comportamiento del tránsito a nivel microscópico y a encontrar las
propiedades que nos pueden indicar de qué manera ciertas configuraciones de
células se comportarán a través del tiempo es el diagrama de ciclos. En
las figuras 4.14, 4.15 y 4.16 se muestran algunos de los ciclos encontrados en
la regla 184 y estos van desde los que se repiten en una generación hasta los
que se repiten en diez generaciones. Como se puede observar en las figuras
4.14, 4.15 y 4.16, un autómata celular contiene ciclos con
características diferentes.
Algunos ciclos representan una
función sobreyectiva como el compuesto por las configuraciones 6, 9, 5, 10, 3
y 12 las cuales forman un ciclo de periodo 2. Otros ciclos representan una
función biyectiva como el compuesto por las configuraciones 2, 1, 8 y 4 las
cuales forman un ciclo de periodo 4.
A diferencia de los anillos
que representan secuencias con diferentes desplazamientos, lo cual fue
explicado anteriormente, los nodos de los diagramas de ciclos representan
configuraciones globales dentro de la evolución del autómata. Esto nos
sirve para identificar ancestros, es decir, si tenemos una configuración
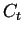 por medio de los diagramas de ciclos podemos conocer cuántas y cuáles
configuraciones la pueden generar en
por medio de los diagramas de ciclos podemos conocer cuántas y cuáles
configuraciones la pueden generar en 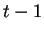 . Por ejemplo, si tenemos la
configuración 11011 podemos saber que esta configuración tiene cuatro
ancestros en los tiempos
. Por ejemplo, si tenemos la
configuración 11011 podemos saber que esta configuración tiene cuatro
ancestros en los tiempos
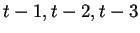 y
y 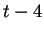 ; estas configuraciones
son: 10111, 01111, 11110 y 11101. Esto puede ser muy útil para analizar el
flujo de tránsito puesto que si tenemos una cierta distribución de los
automóviles sobre la carretera podemos determinar paso a paso como se fue
generando ésta en el transcurso del tiempo.
; estas configuraciones
son: 10111, 01111, 11110 y 11101. Esto puede ser muy útil para analizar el
flujo de tránsito puesto que si tenemos una cierta distribución de los
automóviles sobre la carretera podemos determinar paso a paso como se fue
generando ésta en el transcurso del tiempo.
De esta manera el
análisis lo podemos hacer sobre secuencias cortas que nos permiten enfocarnos
al estudio del comportamiento a nivel microscópico de grupos pequeños de
autos o al estudio a nivel macroscópico con configuraciones más grandes.
Por último, podemos ver una simulación de flujo de tránsito
de autos representada mediante un diagrama de espacio-tiempo el cual se obtiene
a través del diagrama de evoluciones del autómata celular.




Next: Comentarios
Up: Analizando la regla de
Previous: Modelo de arranque lento
Contents
rene
2003-10-20
![\includegraphics[width=2.5in]{4-8r}](img194.gif)
![\includegraphics[width=4in]{4-10r}](img196.gif)
![]() . Para que dos nodos puedan estar conectados se sigue
la misma norma explicada en el capítulo anterior, es decir,
los elementos intermedios de las vecindades parciales que
constituyen los nodos fuente y destino deben coincidir para
conformar junto con las células inicial y final de los nodos
origen y destino respectivamente la vecindad completa, en este
caso, de tamaño 5. Estas vecindades, las cuales constituyen la
generación 0 y se observan en la segunda columna de la tabla 4.2
evolucionan a un solo estado en la segunda generación. Para
obtener esto se toma la primer célula de izquierda a derecha y
las células restantes que completan la vecindad. En este caso,
como se está trabajando con un autómata (2,1) se toman las dos
células de la derecha. Aquí es importante señalar que no
se toman los vecinos de la izquierda porque en la evolución de
las secuencias de un diagrama de Bruijn extendido no se toman en
cuenta los límites periódicos. Una vez que se tiene la
vecindad se aplica la regla de evolución y se obtiene la primera
célula de la siguiente generación, posteriormente se toma la
segunda célula de izquierda a derecha y se repite el proceso
hasta completar la secuencia que constituirá la siguiente
generación.
. Para que dos nodos puedan estar conectados se sigue
la misma norma explicada en el capítulo anterior, es decir,
los elementos intermedios de las vecindades parciales que
constituyen los nodos fuente y destino deben coincidir para
conformar junto con las células inicial y final de los nodos
origen y destino respectivamente la vecindad completa, en este
caso, de tamaño 5. Estas vecindades, las cuales constituyen la
generación 0 y se observan en la segunda columna de la tabla 4.2
evolucionan a un solo estado en la segunda generación. Para
obtener esto se toma la primer célula de izquierda a derecha y
las células restantes que completan la vecindad. En este caso,
como se está trabajando con un autómata (2,1) se toman las dos
células de la derecha. Aquí es importante señalar que no
se toman los vecinos de la izquierda porque en la evolución de
las secuencias de un diagrama de Bruijn extendido no se toman en
cuenta los límites periódicos. Una vez que se tiene la
vecindad se aplica la regla de evolución y se obtiene la primera
célula de la siguiente generación, posteriormente se toma la
segunda célula de izquierda a derecha y se repite el proceso
hasta completar la secuencia que constituirá la siguiente
generación.
![]() y el número de artistas
por
y el número de artistas
por ![]() . En el caso del diagrama que utiliza vecindades
parciales de 4 células el número de nodos que contiene el
diagrama aumenta debido a que el tamaño de las vecindades que se
forman al realizar la operación de superposición es 5 y el
radio de vecindad se extiende a 2 vecinos de cada lado. Por lo
tanto, el número de nodos es
. En el caso del diagrama que utiliza vecindades
parciales de 4 células el número de nodos que contiene el
diagrama aumenta debido a que el tamaño de las vecindades que se
forman al realizar la operación de superposición es 5 y el
radio de vecindad se extiende a 2 vecinos de cada lado. Por lo
tanto, el número de nodos es ![]() y el número de
artistas es
y el número de
artistas es
![]() . Lo anterior se aplica para
determinar el número de nodos y de aristas de cualquier diagrama
de Bruijn extendido. Luego, la matriz de conectividad del diagrama de la
figura 4.11 se define de la siguiente manera:
. Lo anterior se aplica para
determinar el número de nodos y de aristas de cualquier diagrama
de Bruijn extendido. Luego, la matriz de conectividad del diagrama de la
figura 4.11 se define de la siguiente manera: