



Next: Diagramas de Bruijn extendidos
Up: Analizando la regla de
Previous: Generalización
Contents
El modelo SIS para tránsito consiste de un solo
carril uni-direccional en el cual los autos no pueden moverse
hasta después de haberse detenido y haber esperado por una
unidad de tiempo. El número de autos bloqueados por los autos
que están en 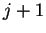 en el tiempo
en el tiempo 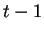 se representa por
se representa por
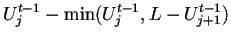 . Esos autos no
pueden moverse en el tiempo
. Esos autos no
pueden moverse en el tiempo 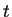 ; por lo tanto el máximo número
de autos que se pueden mover al sitio
; por lo tanto el máximo número
de autos que se pueden mover al sitio 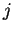 en el tiempo
en el tiempo 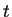 es dado
por
es dado
por
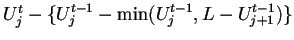 .
De esta forma, la generalización del AC SIS es dada por la
ecuación
.
De esta forma, la generalización del AC SIS es dada por la
ecuación
![$\displaystyle U^{t+1}_j = U^t_j + {\rm min}[U^t_{j-1} - \{U^{t-1}_{j-1} -
{\rm min}(U^{t-1}_{j-1}, L - U^{t-1}_j)\}, L - U^t_j]$](img189.gif) |
|
|
|
![$\displaystyle -
{\rm min}[U^t_j - \{U^{t-1}_j - {\rm min}(U^{t-1}_j, L - U^{t-1}_{j+1})\}, L -
U^t_{j+1}].$](img190.gif) |
|
|
(4.3) |
Esta generalización incluye el modelo original de Takayasu y
Takayasu [91] en el caso de que 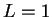 . Puesto que
. Puesto que
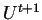 es determinada por
es determinada por 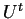 y
y 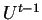 , la ecuación de
evolución es de segundo orden en tiempo, de esta forma se
incluye una inercia de autos en el modelo.
, la ecuación de
evolución es de segundo orden en tiempo, de esta forma se
incluye una inercia de autos en el modelo.
Existen
otros modelos que contemplan la posibilidad de que los autos
avancen más de un sitio a la vez, un ejemplo de este tipo de
modelos son el EBCA1 y EBCA2 [72], los cuales son
extensiones del Autómata Celular Burger (BCA). En esta tesis no
se analizan todos los modelos existentes puesto que el objetivo no
es encontrar el que ofrezca las mejores características en
cuanto a fluidez sino mostrar una perspectiva de análisis que
permita estudiar cualquier modelo o autómata que represente el
comportamiento del tránsito de autos.
En la
siguiente sección se ilustra lo anterior analizando la regla de
AC(2,1) 184.




Next: Diagramas de Bruijn extendidos
Up: Analizando la regla de
Previous: Generalización
Contents
rene
2003-10-20