Sin duda alguna uno de los trabajos más elegantes y sobresalientes es el denominado ``Endomorphisms and Automorphisms of the Shift Dynamical Systems'' publicado por Gustav A. Hedlund en 1969 [Hedlund 69]. El escrito se presenta elegantemente mediante una exposición de dinámica simbólica y sistemas dinámicos de corrimiento. Los análisis de los sistemas dinámicos de corrimiento a través de sus aspectos topológicos y teóricos de medida permite llegar a resultados muy relevantes.
La elegancia del teorema fundamental de estructura hace posible la derivación de numerosos resultados concernientes a las transformaciones de corrimientos conmutativos.
La estructura local relacionada con la estructura global resulta ser una cuestión importante que se presenta en cualquier sistema dinámico en donde la existencia y las propiedades de las transformaciones contínuas conmutan con el grupo de acción. La inducción de un mapeo global a partir de uno local se presenta a través de la definición de un mapeo de bloques (palabras) de símbolos de una longitud específica en símbolos simples y extendiendo este mapeo en una manera natural en secuencias infinitas.
En el análisis de los autómatas celulares lineales reversibles, debemos empezar por conocer las propiedades que cumplen los autómatas sin Jardín del Edén, es decir, donde toda secuencia tenga al menos un ancestro. Relacionado a esta idea, en el trabajo de Hedlund encontramos un concepto fundamental al cual él denomina Multiplicidad Uniforme.
La multiplicidad uniforme en un autómata celular reversible nos dice que cada cadena de estados tiene el mismo número de ancestros que las demás cadenas; y este número es igual al número de nodos del diagrama de de Bruijn.
Se parte de un autómata celular reversible
![]() , con las siguientes convensiones:
, con las siguientes convensiones:
En seguida vamos a parafrasear algunos de los resultados más importantes del trabajo de Hedlund [Hedlund 69]. La indicación (Resultado ![]() ) en cada uno de los siguientes enunciados indica la sección en que aparece el mismo enunciado en el trabajo original de Hedlund.
) en cada uno de los siguientes enunciados indica la sección en que aparece el mismo enunciado en el trabajo original de Hedlund.
Nuestro interés es usar estos resultados dentro del contexto de los autómatas celulares lineales. La relevancia para los casos reversibles estriba en que los siguientes resultados nos indicarán cuales son las propiedades que tienen los autómatas celulares sin Jardín del Edén. El primer resultado nos dá un comportamiento cuantitativo de los ancestros de una cadena y se presenta a contunuación.
Prueba: Tomemos a
![]() ; tomemos a
; tomemos a ![]() como las secuencias formadas al concatenar
como las secuencias formadas al concatenar ![]() con todo elemento de
con todo elemento de ![]() . Si
. Si
![]() , entonces
, entonces
![]() lo cual cubre todas las posibilidades de ancestros de
lo cual cubre todas las posibilidades de ancestros de ![]() .
.
Para una cadena
![]() , su evolución,
, su evolución, ![]() pertenece a
pertenece a ![]() si y solo si
si y solo si ![]() es un bloque de longitud
es un bloque de longitud ![]() tal que
tal que ![]() , es decir, si
, es decir, si
![]() .
.
De este modo el número de ancestros de las secuencias ![]() está dado por la suma de los ancestros de toda posible secuencia
está dado por la suma de los ancestros de toda posible secuencia ![]() ; es decir:
; es decir:
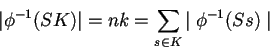 |
(3.1) |
Sabemos por el enunciado que
![]() para cada
para cada ![]() . Si para cualquier
. Si para cualquier ![]() , se cumple que
, se cumple que
![]() , se tiene entonces que
, se tiene entonces que
![]() lo cual es una contradicción.
lo cual es una contradicción.
De aquí concluimos que
![]() para
cada
para
cada ![]() .
. ![]()
Lo que indica el resultado anterior es que en un autómata celular lineal reversible, el número de ancestros de cualquier secuencia se mantendrá igual no importando que tanto extendamos la misma. Una cuestión importante ahora, es conocer cual es este número de ancestros, esto se responderá en el siguiente resultado.
Prueba: Definamos los siguientes conjuntos que utilizaremos en la demostración:
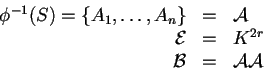
Como cada
![]() tiene tantos elementos como
tiene tantos elementos como ![]() , cada
, cada
![]() es de longitud
es de longitud ![]() y su evolución,
y su evolución, ![]() , es de longitud
, es de longitud ![]() .
.
Ya que
![]() , se tiene que
, se tiene que ![]() es de la forma
es de la forma ![]() ; donde
; donde
![]() aparece en medio de cada evolución de
aparece en medio de cada evolución de ![]() . Es decir,
. Es decir,
![]() .
.
Toda evolución de cualquier secuencia ![]() pertenece al conjunto
pertenece al conjunto ![]() sin que falte ningún elemento de
sin que falte ningún elemento de ![]() pues el mapeo global es sobreyectivo (no existe el Jardín del Edén), en otras palabras, todos los ancestros del conjunto
pues el mapeo global es sobreyectivo (no existe el Jardín del Edén), en otras palabras, todos los ancestros del conjunto ![]() están contenidos en el conjunto
están contenidos en el conjunto ![]() . Es decir,
. Es decir,
![]() ; de aquí llegamos a que:
; de aquí llegamos a que:
| (3.2) |
Dado que
![]() , se tiene que
, se tiene que
![]() .
.
Del enunciado, sabemos que
![]() para cada
para cada
![]() con
con
![]() . Si tomamos en cuenta todos los ancestros de
. Si tomamos en cuenta todos los ancestros de ![]() entonces
entonces
![]() .
.
De este modo llegamos a que ![]() , por lo que
, por lo que ![]() .
. ![]()
Lo que este resultado nos aporta es que si el número de ancestros de una secuencia se mantiene para las extensiones de la misma, este número es igual a ![]() . Haciendo uso de los dos resultados anteriores, hagamos una generalización del comportamiento cuantitativo de los ancestros en un autómata celular lineal reversible.
. Haciendo uso de los dos resultados anteriores, hagamos una generalización del comportamiento cuantitativo de los ancestros en un autómata celular lineal reversible.
Prueba: Para ![]() y
y
![]() , definamos a
, definamos a
![]() como el conjunto de secuencias de longitud
como el conjunto de secuencias de longitud ![]() . Por el hecho de que el autómata es reversible, el mapeo entre configuraciones es sobreyectivo, por lo que toda secuencia de estados tiene al menos un ancestro.
. Por el hecho de que el autómata es reversible, el mapeo entre configuraciones es sobreyectivo, por lo que toda secuencia de estados tiene al menos un ancestro.
Tomemos a ![]() como el mínimo número de ancestros que tenga alguna
como el mínimo número de ancestros que tenga alguna
![]() . Para dicha secuencia, el valor de
. Para dicha secuencia, el valor de ![]() se mantendrá (resultado 1) cumpliendo además que
se mantendrá (resultado 1) cumpliendo además que ![]() (resultado 2).
(resultado 2).
Todos los posibles ancestros de ![]() se encuentran en el conjunto
se encuentran en el conjunto ![]() ; el total de número de elementos de este conjunto es
; el total de número de elementos de este conjunto es
![]() . Por otro lado, dado que
. Por otro lado, dado que ![]() es el mínimo número de ancestros de toda cadena en
es el mínimo número de ancestros de toda cadena en ![]() , y como
, y como
![]() , entonces minimamente hay tantos ancestros como
, entonces minimamente hay tantos ancestros como ![]() con
con ![]() .
.
Si existe alguna cadena en ![]() con un número de ancestros mayor que
con un número de ancestros mayor que ![]() , entonces se cumple que
, entonces se cumple que
![]() lo cual no puede ser pues no hay mas ancestros que
lo cual no puede ser pues no hay mas ancestros que
![]() . Por lo tanto cada cadena en
. Por lo tanto cada cadena en ![]() tiene
tiene ![]() ancestros con
ancestros con ![]() .
. ![]()
Por los resultados anteriores sabemos entonces cual es el número de ancestros de una secuencia y que este valor es el mismo para todas las demás secuencias de un autómata celular lineal reversible. Hay que señalar que el número de ancestros concuerda con el número de nodos en el diagrama de de Bruijn.