

Para ver como funcionan todos los resultados anteriores tomemos un autómata reversible ![]() con
con ![]() y
y
![]() . En ambos casos las dos reglas tienen el mismo valor de
. En ambos casos las dos reglas tienen el mismo valor de ![]() y, por lo tanto, el mismo tamaño de vecindad,
y, por lo tanto, el mismo tamaño de vecindad, ![]() .
.
Se ve que cada estado tiene la misma probabilidad de generarse que el resto tanto en ![]() como en
como en ![]() ; tomemos varias cadenas aleatorias de elementos y veamos cuales son sus ancestros para
; tomemos varias cadenas aleatorias de elementos y veamos cuales son sus ancestros para ![]() .
.
En todos los casos se observa que el número de ancestros es igual a
![]() . Ahora analizemos las distintas partes de los ancestros para dichas cadenas.
. Ahora analizemos las distintas partes de los ancestros para dichas cadenas.
Se puede observar que en todos los casos se cumple que ![]() ,
, ![]() y
y ![]() ; con
; con ![]() . Se cumple que las diferencias de los ancestros se presenten a los extremos, dejando una parte central única. Ahora observemos el diagrama de de Bruijn asociado a la regla de evolución.
. Se cumple que las diferencias de los ancestros se presenten a los extremos, dejando una parte central única. Ahora observemos el diagrama de de Bruijn asociado a la regla de evolución.
Cada liga aparece el mismo número de veces que las demás, si tomamos las ligas que forman la secuencia ![]() , observamos lo siguiente:
, observamos lo siguiente:
Esta ruta tiene ![]() posibles nodos iniciales
posibles nodos iniciales ![]() , comparten un único nodo central
, comparten un único nodo central ![]() indicando que
indicando que ![]() y terminan en
y terminan en ![]() nodos distintos
nodos distintos ![]() .
.
Tomemos ahora el diagrama de parejas de dicho autómata:
Si editamos este diagrama de modo que solo presentemos los ciclos que existen en él obtenemos la siguiente construcción.
Los únicos ciclos que existen aparecen en la diagonal principal que es el diagrama de de Bruijn mismo, y aparte de esto no se presentan de ninguna otra forma, lo que indica que no es posible construir una secuencia de longitud indefinida de ![]() o más modos distintos.
o más modos distintos.
Los diagramas de subconjuntos de la regla original y la regla reflejada son los siguientes:
Para la regla original el máximo nivel que se puede alcanzar empezando desde las clases unitarias es el nivel ![]() , lo que indica que
, lo que indica que ![]() , y de ahí, estas mismas rutas no salen de este nivel. Lo mismo ocurre con las clases unitarias del diagrama de la regla reflejada, en donde el máximo nivel al que se arriba es el
, y de ahí, estas mismas rutas no salen de este nivel. Lo mismo ocurre con las clases unitarias del diagrama de la regla reflejada, en donde el máximo nivel al que se arriba es el ![]() también, mostrando que
también, mostrando que ![]() y tampoco estas rutas abandonan este nivel. Editemos los diagramas y tomemos los conjuntos que están auto-ligados en estos niveles.
y tampoco estas rutas abandonan este nivel. Editemos los diagramas y tomemos los conjuntos que están auto-ligados en estos niveles.
De esta forma obtenemos los diagramas de Welch del autómata ![]() regla
regla ![]() . Veamos ahora en el diagrama derecho las rutas de la secuencia
. Veamos ahora en el diagrama derecho las rutas de la secuencia ![]() y en el diagrama izquierdo las rutas de la secuencia
y en el diagrama izquierdo las rutas de la secuencia ![]() .
.
Ambas rutas convergen a un único nodo, estos nodos finales tiene un solo elemento en común que es ![]() ; es decir, que la secuencia
; es decir, que la secuencia ![]() regresa hacia atrás en la evolución con el estado
regresa hacia atrás en la evolución con el estado ![]() como se vio anteriormente. Del diagrama de de Bruijn obtengamos la matriz de conectivdad de
como se vio anteriormente. Del diagrama de de Bruijn obtengamos la matriz de conectivdad de ![]()
![]()
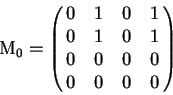
En esta matriz existen
![]() elementos distintos de
elementos distintos de ![]() . Ahora bien, si elevamos
. Ahora bien, si elevamos ![]() al cuadrado, obtenemos la matriz de conectividad de la secuencia
al cuadrado, obtenemos la matriz de conectividad de la secuencia ![]() denotada como
denotada como
![]() .
.
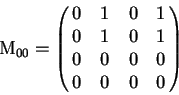
Vemos que el número de elementos distintos de ![]() sigue siendo
sigue siendo ![]() cumpliendo con la multiplicidad uniforme, además, los renglones distintos de
cumpliendo con la multiplicidad uniforme, además, los renglones distintos de ![]() son
son ![]() y las columnas distintas de
y las columnas distintas de ![]() son
son ![]() indicando cuales son los nodos iniciales y finales de esta ruta. En ambos casos la suma de renglones distintos de
indicando cuales son los nodos iniciales y finales de esta ruta. En ambos casos la suma de renglones distintos de ![]() es igual a
es igual a ![]() y la suma de columnas con la misma propiedad es
y la suma de columnas con la misma propiedad es ![]() . Ahora vamos a resolver el problema de eigenvalores para la matriz de conectividad
. Ahora vamos a resolver el problema de eigenvalores para la matriz de conectividad
![]() . Calculando los eigenvalores tenemos
. Calculando los eigenvalores tenemos
![]() .
.
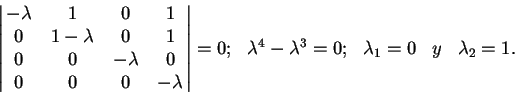
Los eigenvalores que se obtienen son ![]() de multiplicidad tres que es el caso trivial y
de multiplicidad tres que es el caso trivial y ![]() el cual indica que si elevamos esta matriz, equivalente a obtener la matriz de conectividad de una secuencia formada concatenando el mismo estado repetidamente, se seguirá conservando el mismo número de ancestros.
el cual indica que si elevamos esta matriz, equivalente a obtener la matriz de conectividad de una secuencia formada concatenando el mismo estado repetidamente, se seguirá conservando el mismo número de ancestros.
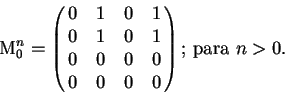
En todos los casos el número de elementos distintos a ![]() es
es ![]() . Ahora obtengamos el eigenvector-renglón de
. Ahora obtengamos el eigenvector-renglón de ![]() denotado por
denotado por
![]() y el eigenvector-columna de
y el eigenvector-columna de ![]() transpuesta que denotaremos con
transpuesta que denotaremos con
![]() .
.
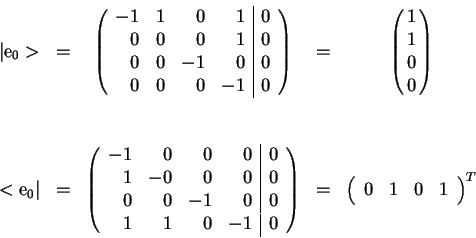
Si multiplicamos ambos eigenvectores obtenemos la siguiente matriz:
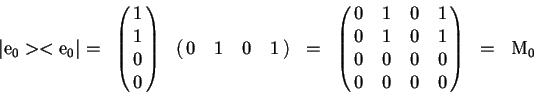
Esta es la matriz de conectividad de la secuencia ![]() obtenida anteriormente, la cual hemos podido reconstruir por medio de los eigenvectores.
obtenida anteriormente, la cual hemos podido reconstruir por medio de los eigenvectores.
Trabajemos con estados distintos, tomemos la matriz de conectividad del estado ![]() .
.
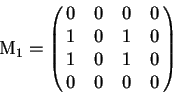
Obtengamos los eigenvalores de la matriz de conectividad de la secuencia ![]() y del estado
y del estado ![]() .
.
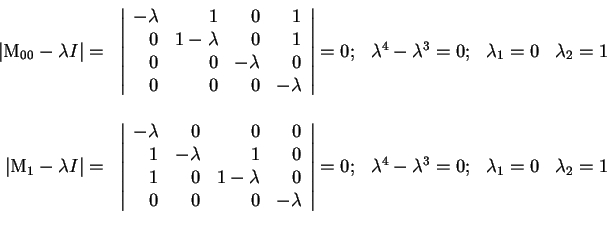
Los eigenvalores no triviales en ambos casos son iguales a ![]() ; calculemos el eigenvector-renglon de
; calculemos el eigenvector-renglon de ![]() y el eigenvector-columna de
y el eigenvector-columna de
![]() .
.
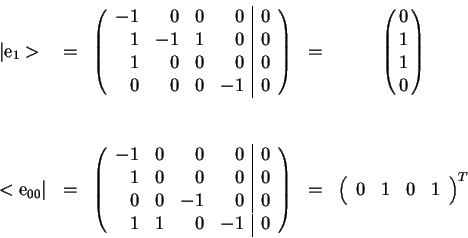
Multiplicando el eigenvector-renglon
![]() con el eigenvector-columna
con el eigenvector-columna
![]() se obtiene la siguiente matriz.
se obtiene la siguiente matriz.
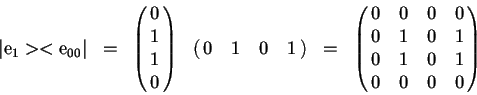
Si tomamos las matrices de conectividad de ![]() y de
y de ![]() y las multiplicamos en el orden que indica la secuencia
y las multiplicamos en el orden que indica la secuencia ![]() obtenemos:
obtenemos:
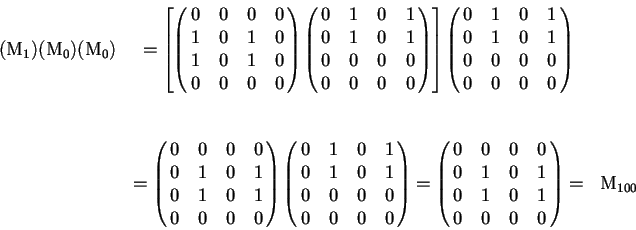
Que fue la matriz que obtuvimos por eigenvectores anteriormente.