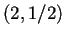 Regla
Regla 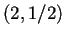 Regla
Regla
Tomemos nuevamente el caso de un auómata de 2 estados y un radio de vecindad ![]() , cuya regla original
, cuya regla original ![]() es un corrimiento a la derecha y la regla inversa
es un corrimiento a la derecha y la regla inversa ![]() es por supuesto, un corrimiento a la izquierda, sabiendo que los indices de Welch tiene valores
es por supuesto, un corrimiento a la izquierda, sabiendo que los indices de Welch tiene valores ![]() y
y ![]() para la regla
para la regla ![]() y
y ![]() y
y ![]() para la regla
para la regla ![]() .
.
Formemos las posibles secuencias de tamaño ![]() , es decir, de
, es decir, de ![]() estados y todos los ancestros de tamaño
estados y todos los ancestros de tamaño ![]() , o sea de
, o sea de ![]() estados, de cada secuencia.
estados, de cada secuencia.
De las secuencias anteriores y sus ancestros, obtengamos los conjuntos ![]() y
y ![]() .
.
En ambos casos se cumple que
![]() y
y
![]() .
.
Tomemos ahora los conjuntos ![]() y
y
![]() , y especifiquemos los siguientes mapeos
, y especifiquemos los siguientes mapeos ![]() y
y ![]() .
.
Como ![]() y
y ![]() , con estos elementos podemos formar entonces las permutaciones
, con estos elementos podemos formar entonces las permutaciones ![]() y
y ![]() .
.
A partir de una configuración aleatoria inicial podemos ver una evolución típica de este autómata ![]() .
.
Tomemos la primera configuración y apliquemos la permutación ![]() .
.
Sobre esta nueva secuencia de la forma
![]() usemos
usemos ![]() , es decir, hagamos un corrimiento de un elemento y apliquemos a cada pareja de la forma
, es decir, hagamos un corrimiento de un elemento y apliquemos a cada pareja de la forma ![]() la permutación
la permutación ![]() .
.
![\includegraphics[width= 400pt]{capitulo3/ps/evolucion2h3.ps}](img579.gif) |
En este caso podemos concluir que la evolución obtenida anteriormente coincide con la construida haciendo dos permutaciones en bloque a la configuración inicial, es decir, el método funcionó como se esperaba en este ejemplo.