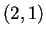 Regla
Regla 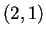 Regla
Regla
Este es el caso de un auómata de 2 estados y un radio de vecindad ![]() , con la regla de evolución
, con la regla de evolución ![]() y la regla inversa
y la regla inversa ![]() . Para la regla
. Para la regla ![]() los indices de Welch tiene valores
los indices de Welch tiene valores ![]() y
y ![]() , para la regla
, para la regla ![]() ,
, ![]() y
y ![]() son los índices de Welch.
son los índices de Welch.
|
De manera análoga al primer ejemplo, se obtuvieron los conjuntos ![]() y
y ![]() .
.
Cumpliéndose en ambos casos se cumple que
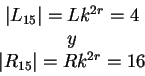
Tomemos ahora los conjuntos
![]() y
y
![]() . Especificando los mapeos
. Especificando los mapeos ![]() y
y ![]() , los podemos ver con detalle en la siguiente tabla.
, los podemos ver con detalle en la siguiente tabla.
Como ![]() y
y ![]() , con estos elementos podemos formar entonces las permutaciones
, con estos elementos podemos formar entonces las permutaciones ![]() y
y ![]() .
.
A partir de una configuración aleatoria inicial, vamos a observar primero como evoluciona el autómata. Empezando desde el instante ![]() hasta llegar al instante
hasta llegar al instante ![]() . Después tratemos de reproducir este resultado por medio de las permutaciones en bloque.
. Después tratemos de reproducir este resultado por medio de las permutaciones en bloque.
Para este caso nuestra conclusión es que la evolución del autómata es idéntica a la construida aplicando las dos permutaciones en bloque a la configuración inicial.