



Next: Lista de Tablas
Up: Caracterización del Comportamiento de
Previous: Bibliografía
Contenido
- Vecindad de von Neumann
- Vecindad de Moore
- Ejemplo de una evolucion de Life
- Clases de Wolfram
- Mecanismo de evolución de un autómata celular lineal tanto en vecindades impares como pares.
- Ejemplo de una evolución del autómata
 regla
regla 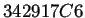
- Diagrama de de Bruijn y su representación matricial para la regla
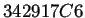
- Ancestros de la cadena
 en el diagrama de de Bruijn
en el diagrama de de Bruijn
- Diagrama de parejas del autómata
 regla
regla 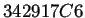
- Ancestros de la secuencia
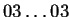
- Diagrama de subconjuntos del autómata
 regla
regla 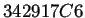
- Laconfiguración
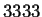 pertenece al jardín del Edén
pertenece al jardín del Edén
- Autómata
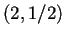 reversible, cuya regla original es
reversible, cuya regla original es 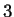 y regla inversa
y regla inversa 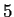 . De una configuración inicial, evoluciona a una configuración dada tal que aplicando la regla inversa se pueda retornar a la configuración original
. De una configuración inicial, evoluciona a una configuración dada tal que aplicando la regla inversa se pueda retornar a la configuración original
- El mapeo biyectivo entre configuraciones globales define un autómata celular reversible
-
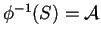 y
y
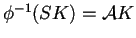
- Si
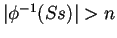 para alguna
para alguna 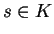 no se cumple que
no se cumple que
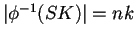
- Ancestros de las secuencias
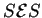
- El total de ancestros de
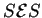 es
es 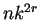
- Ancestros de
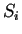 , en donde
, en donde 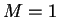
- Ancestros de la secuencia
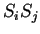 con
con
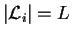 y
y
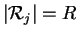
- Ancestros de
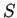 con
con
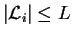 y
y
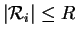
- Si
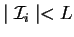 entonces
entonces
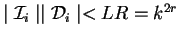 contradiciendo a la multiplicidad uniforme
contradiciendo a la multiplicidad uniforme
- Extensiones de
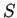 siguen conservando el valor de los índices
siguen conservando el valor de los índices  y
y 
- Si
 entonces la cadena pertenece al jardín del edén y el autómata no es reversible
entonces la cadena pertenece al jardín del edén y el autómata no es reversible
- Si
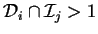 entonces la cadena tiene más ancestros que
entonces la cadena tiene más ancestros que 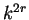 contradiciendo la multiplicidad uniforme
contradiciendo la multiplicidad uniforme
- Autómata celular lineal reversible
 regla
regla 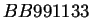
- Ancestros de diversas cadenas
- Indices de Welch para los ancestros del autómata

- Diagrama de de Bruijn del autómata reversible
 , regla
, regla 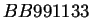
- Rutas posibles de la secuencia
- Diagrama de Parejas del autómata reversible
 , regla
, regla 
- Diagrama de Parejas editado mostrando solamente sus ciclos
- Diagramas de subconjuntos del autómata reversible
 , regla
, regla 
- Diagramas de Welch del autómata
 regla
regla 
- Rutas de la secuencia
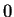 en los diagramas de Welch
en los diagramas de Welch
- Autómata
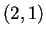 regla
regla 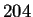
- Elementos de
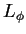 y
y 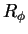
- Composición de dos reglas de evolución
- Composición de las reglas 204 y 15 en el autómata
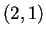
- Permutación
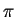 de un bloque de tamaño
de un bloque de tamaño 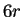
- Representación del funcionamiento de un autómata reversible por medio de dos permutaciones en bloque y un corrimiento
- Evolución de un autómata
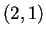 regla
regla 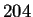
- Funcionamiento de las permutaciones en bloque en el autómata
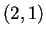 regla
regla 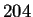
- Aplicando
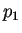 a una configuración inicial aleatoria
a una configuración inicial aleatoria
- Aplicando
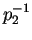 después de
después de 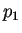 con un corrimiento de
con un corrimiento de 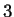 posiciones
posiciones
- Evolución final producida por dos permutaciones en bloque
- Evolución de un autómata
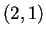 regla
regla 
- Permutación en bloque
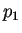 sobre la configuración inicial
sobre la configuración inicial
- Permutación
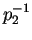 con un corrimiento de tamaño
con un corrimiento de tamaño 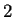
- Funcionamiento de un autómata
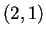 regla
regla 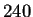 por medio de dos permutaciones en bloque
por medio de dos permutaciones en bloque
- Evolución de un autómata reversible por medio de dos permutaciones en bloque y un corrimiento de tamaño
- Evolución de un autómata
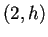 regla
regla 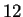
- Permutación en bloque
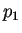 sobre la configuración inicial
sobre la configuración inicial
- Permutación en bloque
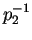 después de
después de 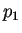 con un corrimiento igual a
con un corrimiento igual a 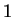 equivalente a una longitud de
equivalente a una longitud de 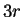
- Evolución de un autómata
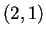 con regla
con regla 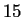 , aplicando las permutaciones en bloque
, aplicando las permutaciones en bloque
- Autómata
 con regla de evolución
con regla de evolución 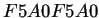 , aplicando las permutaciones en bloque
, aplicando las permutaciones en bloque
- Autómata reversible
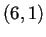 resultado del producto cartesiano de un autómata
resultado del producto cartesiano de un autómata 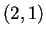 y un autómata
y un autómata 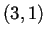
- Evolución del autómata
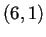
- Evolución del autómata
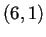
- Estructura de un autómata reversible con
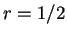
- Estructura de un autómata reversible con
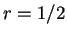
- Tres células y su evolución
- Vecindad inversa formada por
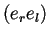
- Bloques que forman los conjuntos
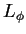 y
y 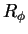
- Permutación
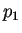 que se especifica con los bloques
que se especifica con los bloques 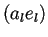 y
y 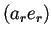
- Permutación
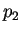 que se especifica con los bloques
que se especifica con los bloques 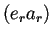 y
y 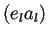
- Diagramas de Welch del autómata reversible
 regla
regla 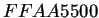
- Evolución del autómata celular reversible
 regla
regla 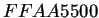 aplicando
aplicando 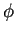 y utilizando las permutaciones en bloque
y utilizando las permutaciones en bloque 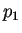 y
y 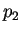
- Diagramas de Welch del autómata reversible
 regla
regla 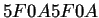
- Evolución del autómata celular reversible
 regla
regla 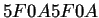 aplicando
aplicando 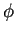 y utilizando las permutaciones en bloque
y utilizando las permutaciones en bloque 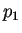 y
y 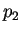
- Diagramas de Welch del autómata reversible
 regla
regla 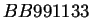
- Evolución del autómata celular reversible
 regla
regla 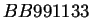 aplicando
aplicando 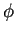 y utilizando las permutaciones en bloque
y utilizando las permutaciones en bloque 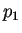 y
y 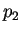
- Diagramas de Welch del autómata reversible
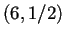 regla
regla
- Evolución del autómata celular reversible
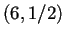 regla
regla
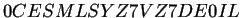 aplicando
aplicando 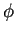 y utilizando las permutaciones en bloque
y utilizando las permutaciones en bloque 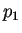 y
y 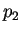
- Diagramas de Welch del autómata reversible
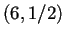 regla
regla
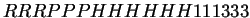
- Evolución del autómata celular reversible
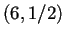 regla
regla
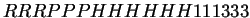 aplicando
aplicando 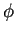 y utilizando las permutaciones en bloque
y utilizando las permutaciones en bloque 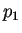 y
y 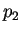
- Diagramas de Welch del autómata reversible
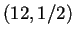
- Evolución del autómata celular reversible
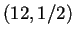 aplicando
aplicando 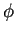 y utilizando las permutaciones en bloque
y utilizando las permutaciones en bloque 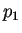 y
y 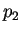
- Diagramas de Welch del autómata reversible
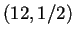
- Evolución del autómata celular reversible
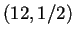 aplicando
aplicando 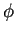 y utilizando las permutaciones en bloque
y utilizando las permutaciones en bloque 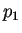 y
y 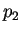
- Autómata
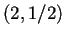 regla
regla 
- Evolución del autómata
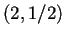 con permutaciones en bloque
con permutaciones en bloque
- Evolución del autómata
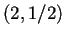 con distintas permutaciones en bloque
con distintas permutaciones en bloque
- Secuencia formada concatenando el estado
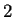 y sus ancetros
y sus ancetros
- Diagrama de de Bruijn del autómata celular lineal reversible
 regla
regla 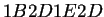
- Diagrama de parejas del autómata celular lineal reversible
 regla
regla 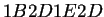
- Diagramas de subconjuntos del autómata
 regla
regla 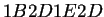 y su reflexión
y su reflexión
- Diagramas de Welch del autómata celular lineal reversible
 regla
regla 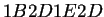
- Cadenas de longitud
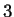 y sus ancestros
y sus ancestros
- Diagramas de parejas y de subconjuntos del autómata
 regla
regla 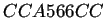
- Estructura de los ancestros de una cadena en el diagrama de de Bruijn para un autómata reversible
- Si
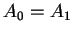 entonces no existe un elemento único común en las rutas
entonces no existe un elemento único común en las rutas
- Si
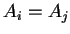 la secuencia de
la secuencia de
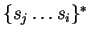 o
o
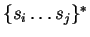 )tendrá más de una variante interna posible
)tendrá más de una variante interna posible
- Si
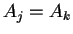 la secuencia de
la secuencia de
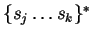 tendrá más de una variante interna posible
tendrá más de una variante interna posible
- Autómata
 regla
regla 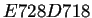 y sus diagramas de Welch
y sus diagramas de Welch
- Rutas del diagrama de de Bruijn de la forma
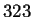
- Ruta
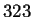 en el diagrama de subconjuntos del autómata
en el diagrama de subconjuntos del autómata  regla
regla 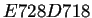
- Autómata
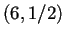 regla
regla
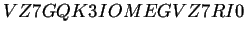 y sus diagramas de Welch
y sus diagramas de Welch
- Rutas del diagrama de de Bruijn de la forma
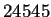
- Ruta
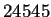 en el diagrama de subconjuntos del autómata
en el diagrama de subconjuntos del autómata 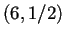 regla
regla
ice
2001-08-31