 |
The doubling method works, but it is clumsy and inefficient. In order to make the manufacture of flexagons more readily practicable, a method has been developed for building a flexagon of any size, with any given map.
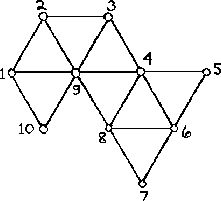
So that we may learn by example, let's pick a map at random: that shown in figure 14. Notice that every side of the flexagon is touched by just two of the map's outer edges. To start the figuring, a network of lines must be drawn throughout the map, made up of the lines joining the midpoints of the map lines. One straight line is continued as long as possible, and is then broken and continued. The drawing of the network is shown in figure 15. This network is known as the Tukey triangle network, named after its inventor, John W. Tukey.
Next, each side must be numbered, in sequence, around the edge of the map, as in figure 14. Then the vertex of the Tukey triangle network between ``1'' and ``2'' is labeled ``1,'' that between ``2'' and ``3'' is labeled ``2,'' and generally that between ``n'' and ``n + 1'' is labeled ``n.'' This is demonstrated in figure 15 C.
Now draw a line below the map. Travel over the Tukey triangle network in the manner used in its construction, along the lines, copying down the numbers at the outer vertices alternately on one side of the line and the other, thus:
| 1 | 8 | 4 | 6 | 10 | 1 | ... | |||||||
| 3 | 5 | 7 | 2 | 9 | 3 | ... |
The vertical line indicates one complete traverse of the network. Add +1 to each number of the sequence and place the resulting sum across the line, opposite the number to which 1 was added. Across the line from the highest number in the sequence, place the number ``1.'' This gives us:
| 1 | 4 | 8 | 6 | 4 | 8 | 6 | 3 | 10 | 10 | 1 | 4 | ... | |
| 2 | 3 | 9 | 5 | 5 | 7 | 7 | 2 | 1 | 9 | 2 | 3 | ... |
Every outer vertex in the network occurs at the midpoint of a map line. This line may go in one of three directions, which are spaced 120° apart. In the following discussion, the term ``map direction'' is used to indicate the direction of this line.
Put an ``R'' at vertex ``1.'' If the map direction is the same for vertex ``1'' as for the next vertex along the network (which, in the example, is ``3''), put an R at the second vertex. If it is different, as it is in the example, use an ``L.'' Pass on through the network in this way. If the map direction changes, change from ``R'' to ``L'' or ``L'' to ``R,'' as the case may be. If it remains the same, retain the sign - ``L'' or ``R'' - last used (see figure 16).
Now copy each sign beneath the numbers associated with the same network vertex:
| 1 | 4 | 8 | 6 | 4 | 8 | 6 | 3 | 10 | 10 | 1 | 4 | ... | |
| 2 | 3 | 9 | 5 | 5 | 7 | 7 | 2 | 1 | 9 | 2 | 3 | ... | |
| R | L | L | R | L | R | L | R | L | R | R | L | ... |
We are now ready to construct the flexagon.
Make an equilateral triangle with an arrow indicating a side through which to enter. Accordingly, as the first sign is ``R'' or ``L,'' add a new triangle on the right- or left- hand edge of the first triangle, as approached through the arrow. Leave the second triangle on the side indicated by the second sign, and so on (see figure 17). Repeat the sequence twice, copying down the signs anew from the network with each repetition, so that there are three like groups of triangles, tied end to end (see figure 18). Cut out this plan.
Label the triangles on one side of the strip of paper with the numbers on one side of the line and label the same triangles on the other side of the strip with the numbers on the other side of the line. Numbers across the line from each other should be on opposite sides of the triangle associated with the corresponding sign (again see figure 18).
To fold the flexagon up, fold together pairs of like adjacent numbers until just two different kinds of numbers show. Then tape the ends of the plan together. For example, you might fold together all the ``5'' 's, then all the ``7'' 's, then ``10'' 's, ``6'' 's, ``8'' 's, ``4'' 's, ``3'' 's, and ``9'' 's, in that order. This would leave sides ``1'' and ``2'' showing, one on the top and the other on the bottom.
Take another example of the use of this horribly involved but correspondingly efficient system. Suppose we want to make two of the three six-sided flexagons. (Do you find it surprising that there should be more than one? Well, each permutation of the map triangles produces a different flexagon. There are always two more sides than map triangles, so that, for the six-sided flexagon, we must permute four map triangles. The only possible non-equivalent permutations are those shown in figure 19 A). Right now we will make flexagons 2 and 3 (figure 19 A). First we construct the Tukey triangle network (figure 19 B), and then number about the vertices (We won't worry this time about which side on the map is labeled which way.) (see figure 19 C) and mark down the signs (see same figure). Now, copying down all this data, we get:
| 1 | 3 | 2 | 1 | ||||
| 4 | 5 | 6 | 4 | ||||
| R | R | L | L | L | L | R | R |
| 1 | 6 | 3 | 1 | ||||
| 2 | 4 | 5 | 2 | ||||
| R | L | L | R | L | L | R | L |
and adding one to each numerical term:
| 1 | 5 | 3 | 6 | 2 | 1 | 1 | 5 |
| 2 | 4 | 4 | 5 | 3 | 6 | 2 | 4 |
| R | R | L | L | L | L | R | R |
| 1 | 3 | 6 | 5 | 3 | 6 | 1 | 3 |
| 2 | 2 | 1 | 4 | 4 | 5 | 2 | 2 |
| R | L | L | R | L | L | R | L |
Now all we have to do is cut out the plans (figure 19 D). The figure shows the entire plan, with the two repetitions. IMPORTANT: Notice that if the number of sides had been ODD, all the signs would have been REVERSED during the first repetition - try it yourself and see - coming out this way on the second time around the Tukey triangle network. In flexagons with an even number of sides, there is no such disturbance. As an example, look at the complete ``L'' - ``R'' sequence for the five-(odd) sided flexagon:
![]() .
.
When the plans have been finished, they are numbered and folded up by folding together like adjacent numbers. It should be remarked that the numbers for the first repetition in odd-sided flexagons also come reversed, with numbers falling on opposite sides of the strip from the usual position. The numbers may be read off the map in this order. This is the reason for including a small portion of the first repetition each time we write a sequence --- odd-or-evenness must be kept in mind. Again we can use the five-sided flexagon as an example:
| 1 | 3 | 5 | 4 | 4 | 2 | 2 | 1 | 3 | 5 | 1 | 3 | 5 | 4 | 4 |
| 2 | 2 | 1 | 3 | 5 | 1 | 3 | 5 | 4 | 4 | 2 | 2 | 1 | 3 | 5 |