Next: Referencias Up: . Previous: . Contents

Conclusiones

La conclusión más importante de este estudio es, que en la cadena líneal se puede observar un comportamiento exponencial el cual se suprime debido a la simetría de la cadena cíclica, existiendo dos degeneraciones.

Por lo tanto,esta conclusión así como las anteriores pueden ser tomadas en cuenta, al tratar de investigar el comportamiento de modelos más reales. APENDICE A

Debido a la importancia de las gráficas que se presentan en esta tesis, es conveniente dar una explicación más detallada de ellas, ya que así se podrán entender mejor los resultados que se presentan en el desarrollo de este trabajo.

Las gráficas se han divido en tres clases, en donde cada clase nos representa a una parte del comportamiento total de la cadena diatómica. Obteniendose para cada uno de los diferentes casos que se analizan, sus correspondientes tres clases de gráficas.

La primera clase nos representa a los eigenvalores de la matriz de movimiento que físicamente nos representan al cuadrado de las frecuencias características o temporales.

La segunda clase nos representa a los eigenvectores de la matriz de movimiento que físicamente nos representan a los modos normales de vibración.

La tercera clase nos representa a los números de onda o frecuencias espaciales de acuerdo a la siguiente relación de dispersión.

$\begin{displaymath} C = \frac{2[\rho \varepsilon + (K + 2)] \pm \sqrt{4[(\rho ... ...]^{2} + 2 \rho \varepsilon (K + 1) + 2 (K^{2} + 2K + 2)}}{8} \end{displaymath}$

Por lo tanto explicaremos cada clase por separado.
PRIMERA CLASE

Se sabe que el rango donde ocurren los eigenvalores de la matriz de movimiento es $-4 (A_{1} + A_{2}) \leq \lambda \leq 0$ . Por lo que la subrutina PENGR que es con la que se grafica a los eigenvalores de la matriz, está diseñada para que sólo aparezca este rango en la hoja de impresión.

Ahora bién, en el eje horizontal (eje X), se imprimen por medio de números 1, 2, 3 ..... N los valores de las diferentes frecuencias, correspondiendo el 1 a la primera frecuencia, el 2 a la segunda frecuencia, etc. En el eje vertical (Eje Y), se hace la variación del parámetro correspondiente, o sea el número de veces que se incrementará el parámetro; con el fin de obtener una buena información del caso de la cadena que se este analizando el número que se escogió de interacciones fué 41.

Diagrama de flujo del programa principal PENTA

$\includegraphics[width=4in]{imagenes/dia1.eps}$

SEGUNDA CLASE Con el fin de observar, en forma más clara los diferentes movimientos que sufra la cadena, se graficaron los modos normales de vibración, en tres dimensiones en la forma siguiente:

El número de partículas, quedará representado en el eje (X), la amplitud que sufran las partículas en el eje (Z) y en la parte negativa del eje (Y), se verá la variación del parámetro correspondiente. Las discontinuidades de estas gráficas, son reflejo de los cruzamientos que ocurren entre las frecuencias del espectro, y los nodos que se vean en los modos son los cruzamientos que existen con el eje (X) de estas mismas gráficas, siendo el modo de más alta frecuencia, el que tenga mayor número de nodos.

Estas gráficas se obtienen, por medio del programa principal PENHL, el cual está diseñado, para leer los valores que fueron almacenados en el disco, por el programa anterior, de los modos normales y graficarlos por medio del Plotter (graficador).
TERCERA CLASE En la primera parte de este trabajo fué deducida, de la matriz de recurrencia, la siguiente relación de dispersión.

$\displaystyle \mu^{4} - \mu^{3} [K^{2} + 8 (\rho + 1/\rho) + 4(K + 1)] + \mu^{2}[4(K + 1)^{2} - 2K^{2} + 2 +$
$\displaystyle + 2(K + 1) \varepsilon (\rho + 1/\rho) + \varepsilon^{2}] - \mu[\kappa^{2} + \varepsilon (\rho + 1/\rho) + 4(K + 1)] + 1 = 0$			(I-1 )

donde $\varepsilon = \lambda \sqrt{Mm} / A_{2}$

De (A-1) se puede ver que los coeficientes resultan ser simétricos.

Como se sabe que las raíces, de esta relación de dispersión ocurren en parejas recíprocas, entonces definimos:

$\begin{displaymath} r_{1} + \frac{1}{r_{1}} = a \ \ \ \ \ \ \ \ \ \ \ r_{2} + \frac{1}{r_{2}} = b \end{displaymath}$

por lo que en forma factorizada resulta:

$\begin{displaymath} (\mu^{2} - a\mu + 1)(\mu^{2} - b\mu + 1) = 0 \end{displaymath}$

desarrollando

$\begin{displaymath} \mu^{4} - (a + b)\mu^{3} + (2 + a b)\mu^{2} - (a + b)\mu + 1 = 0 \end{displaymath}$

(I-2 )

comparando (A-1) y (A-2), obtenemos las siguientes ecuaciones:

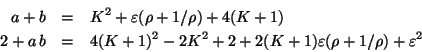
$\begin{eqnarray*} a + b & = & K^{2} + \varepsilon(\rho + 1 /\rho) + 4 (K + 1)\\... ...+ 2 + 2 (K + 1) \varepsilon (\rho + 1 /\rho) + \varepsilon^{2} \end{eqnarray*}$

denotando por $\rho = \rho + \frac{1}{\rho}$ , las ecuaciones anteriores quedan:

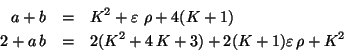
$\begin{eqnarray*} a + b & = & K^{2} + \varepsilon \ \rho + 4(K + 1)\\ 2 + a\,b & = & 2(K^{2} + 4\,K + 3) + 2(K + 1) \varepsilon\,\rho + K^{2} \end{eqnarray*}$

Donde la solución, de estas ecuaciones determinan, los números de onda en función de $\kappa, \rho, \varepsilon$ . Sin embargo podemos resolver, la relación de dispersión para $\varepsilon$ , por lo que despejamos $\varepsilon$ de (A-1) resultando:

$\begin{displaymath} \varepsilon^{2} + 2 \rho \ \varepsilon [K + 1 - C] + 4C^{2} - 2C[K^{2} + 4(K + 1)] + 4(K + 1)^{2} - 2K^{2} = 0 \end{displaymath}$

(I-3 )

donde $2C = \mu + \frac{1}{\mu} \ \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ C = \frac{\... ...{1}{\mu}}{2} = \frac{e^{\varphi} + e^{-\varphi}}{2} = \mbox{cos} \ h \ \varphi$

cuya solución para $\varepsilon$ es:

$\begin{displaymath} \varepsilon = \frac{-2 \rho (K + 1 - K) \pm \sqrt{4\rho^{2}... ...- 2 \varepsilon[K^{2} + 4(K + 1)] + 2K^{2} + 6 K + 4 \}}}{2} \end{displaymath}$

Finalmente nos interesa encontrar, la relación de dispersión en función del parámetro C, por lo que de (A-3) obtenemos, C en función de los parámetros $\varepsilon, \rho$ y $\kappa$ .

$\begin{displaymath} 4C^{2} - 2C(\rho \varepsilon + K^{2} + 4K + 4) + \varepsilon^{2} + 2 \rho \varepsilon(K + 1) + 2(K^{2} + 4(K + 2)) = 0 \end{displaymath}$

(I-4 )

cuya solución es:

$\begin{displaymath} C = \frac{2 (\rho \varepsilon + (K + 2)^{2} \pm \sqrt{4[\rh... ...on^{2} + 2 \rho \varepsilon(K + 1) + 2(K^{2} + 4K + 2)]}}{8} \end{displaymath}$

(I-5 )

Estas soluciones son los números de onda, que graficaremos para ver el comportamiento, desde el punto de vista ondulatorio, de la cadena.

Existiendo cuatro regiones de importancia, para los valores del coseno hiperbólico C, cuya interpretación física fue hecha en la primera parte de esta tesis.

REGION 1 Es cuando $\varphi$ es real, $\mbox{cos} \ h \varphi = \frac{e^{\varphi} + e^{-\varphi}}{2} > 1$ entonces un valor de C es y otro es , siendo en esta región el comportamiento de la cadena, en forma de una exponencial creciente o decreciente, dependiendo que $\varphi > 1$ ó $\varphi < 1$ .

REGION 2 Es cuando es de la forma, $\varphi = i \ \beta$ lo cual implica que

$\begin{displaymath}\mbox{cos} \ h \ \varphi = \mbox{cos} \ h \ i \ \beta = \fra... ...- i \ \mbox{sen}\beta}{2} = \frac{2 \mbox{cos}\beta}{2} \leq 1\end{displaymath}$

entonces los valores de C, estan en el rectángulo $-1 \leq C \leq 1$ , y el comportamiento de la cadena, correspondera a un

, es decir de tipo ondulatorio.

REGION 3 Cuando $\varphi$ es de la forma $\varphi = \alpha + i \pi$ lo cual implica que

$\begin{displaymath}\mbox{cos} \ h (\alpha + i \pi) = \frac{e^{\alpha}(\mbox{cos... ...frac{e^{\alpha} - e^{- \alpha}}{2} = - \mbox{cos} \ h \ \alpha,\end{displaymath}$

entonces los valores de C estarán en el intervalo $-2.0 \leq C \leq 0.5$ , en este caso se observarán oscilaciones con inversiones de fase, producidas por un desfasamiento de $180^{\circ}$ .

REGION 4 Es cuando $\varphi = \alpha + i \beta$ esto implica que

$\begin{displaymath}\mbox{cos} \ h(\alpha + i \ \beta) = \frac{e^{\alpha}(\mbox{... ...eta) + e^{-\alpha} (\mbox{cos} \beta + i \mbox{sen} \beta)}{2}\end{displaymath}$

Por lo que en este caso el comportamiento de la cadena será en forma, cosenoidal o senoidal modulada por el factor exponencial $e^{\alpha}$ , que depende de la parte real de $\varphi$ .

Ahora bien, las gráficas de los números de onda, serán obtenidas por medio del programa principal Pencc, el cual esta diseñado para imprimir marcas (X), que definen la región 2 o sea el rectángulo cuyos vertices son:
(-1,-1), (1,-1),(1,1),(-1,1) y el origen (0,0), quedando así definidas las demas regiones. Esto se hace para cada gráfica. Hagamos un ejemplo, de una gráfica que corresponda a los números de onda, de los valores de alguna frecuencia del espectro.

$\includegraphics[width=4in]{imagenes/fig79.eps}$

Se puede observar, que una parte de la gráfica anterior está definida en la región 2, por lo tanto el comportamiento de la cadena, será en forma senoidal o cosenoidal y se reflejará en alguna parte de la gráfica del modo normal co-rrespondiente, también se ve que en otra parte de la gráfica está definida en la región 1, por lo que el comportamiento de la cadena será en forma exponencial.

//FOR
*I0CS(1403 PRINTER,2501READER,DISK)
*ONE WORD INTEGERS
*LIST ALL
*NAME PENTA
C **************************************************************
C
C                             APENDICE B
C
C                         PROGRAMA PRINCIPAL
C
C                                 PENTA
C
C **************************************************************
C
C  LA DESCRIPCION DE UNO DE LOS PROGRAMAS QUE SE EMPLEARON PARA
C  CALCULAR EL ESPECTRO DE FRECUENCIAS Y LOS MODOS NORMALES DE
C  VIBRACION
C
C           PENTA ES EL PROGRAMA PRINCIPAL QUE NOS CALCULA LOS
C  EIGENVALORES Y EIGENVECTORES DE UNA MATRIZ PENTADIAGONAL A
C  LA CUAL SE PUEDEN HACER MODIFICACIONES EN LAS ESQUINAS DE
C  SUS DIAGONALES
C
C  INSTRUCCIONES DE ENTRADA QUE SIRVEN PARA DEFINIR ARREGLOS,
C  NOMBRES DE VARIABLES Y PARA DEFINIR ARREGLOS EN EL DISCO
C
      DIMENSION   X(12,41)
      DIMENSION   Z(32)
      COMMON      N,LI,LO,XO,XN
      COMMON      D(30),C(30),B(30),A(30),B(30)
      COMMON      Q(4,4),V(31)
      DEFINE FILE 200(12,82,U,IK)
      DEFINE FILE  10(57,120,U,K1)
      DEFINE FILE 101(41,96,U,KO1)
      DEFINE FILE 102(41,96,U,K02)
      DEFINE FILE 103(41,96,U,K03)
      DEFINE FILE 104(41,96,U,K04)
      DEFINE FILE 105(41,96,U,K05)
      DEFINE FILE 106(41,96,U,K06)
      DEFINE FILE 107(41,96,U,K07)
      DEFINE FILE 108(41,96,U,K08)
      DEFINE FILE 109(41,96,U,K09)
      DEFINE FILE 110(41,96,U,K10)
      DEFINE FILE 111(41,96,U,K11)
      DEFINE FILE 112(41,96,U,K12)
      DEFINE FILE 113(41,96,U,K13)
      DEFINE FILE 114(41,96,U,K14)
      DEFINE FILE 115(41,96,U,K15)
      DEFINE FILE 116(41,96,U,K16)
      DEFINE FILE 117(41,96,U,K17)
      DEFINE FILE 118(41,96,U,K18)
      DEFINE FILE 119(41,96,U,K19)
      DEFINE FILE 120(41,96,U,K20)
C
C  INSTRUCCIONES DE ENTRADA PARA LEER LA DIMENSION (N)
C  QUE DESEAMOS ANALIZAR
C
      LI=8
      LO=5
      READ  (LI,20) N
   20 FORMAT(I2)
      IF(N) 2,2,3
    2 CALL EXIT
    3 WRITE    (LO,300) N
  300 FORMAT  ('1N,'I2)
C
C  GENERACION DE LOS ELEMENTOS MATRICIALES .-LLENAMOS LA MATRIZ
C  TENIENDO EN CUENTA SU FORMA PENTADIAGONAL (DIAGONALES A,B,C,
C  D,E) LO CUAL NOS PERMITE UTILIZAR MENOS MEMORIA DE LA MAQUINA,
C  ESTA PARTE ES LA QUEGENERALMENTE DIFIERE DE MODELO A MODELO
C
      F=0.045
      XMG=1,4
      XMP=0.875
      A1=0.1
      A2=1.9
      AO=-2.0*(A1+A2)
      DO 30 K=1,41
      X1=A1/SQRT(XMP*XMG)
      X2=A2/XMP
      X0=A0/XMP
      Y2=A2/XMG
      Y0=A0/XMG
      DO 15 I=1,N,2
      A(I)=X2
      B(I)=X1
      C(I)=X0
      D(I)=X1
   15 E(I)=X2
      DO 16 I=2,N,2
      A(I)=Y2
      B(I)=X1
      C(I)=Y0
      D(I)=X1
   16 E(I)=Y2
C
C  PENII CALCULA LOS LIMITES DE GERSHGORIN DE LOS EIGENVALORES Y
C  FORMA LOS COEFICIENTES USADOS EN LA RELACION DE RECURSION COMO
C  ELEMENTOS DE LAS MATRICES DE TRANSFERENCIA (T)
C
      CALL PENII
C
C  PENRO LOCALIZA LAS RAICES DE LA ECUACION CARACTERISTICA,
C  COLOCANDO A ELLAS EN CIERTO ARREGLO(V)
C
      CALL PENRO
      DO 23 J=1,N
   23 X(J,K)=V(J)
C
C  PENGR (W,Z1,Z2) GRAFICA LOS EIGENVALORES POR MEDIO DE NUMEROS
C  IMPRIMIENDO EL NUMERO DEL EIGENVALOR CORRESPONDIENTE Y Z1,Z2
C  SON LOS LIMITES DE DONDE SE QUIERE VER LA GRAFICA
C
      CALL PENGR (V,0.0,8.0)
C
C        CALCULO DE LOS EIGENVECTORES
C
      DO 12 I=1,N
C
C  PENEV CALCULA LAS COMPONENTES DEL I-ESIMO EIGENVECTOR DEJANDO
C  LAS COMPONENTES EN EL ARREGLO Z
C
      CALL PENEV(Z,I)
C
C  PENNO NORMALIZA LAS PRIMERAS N COMPONENTES DEL VECTOR DEL
C  ARGUMENTO Z

      CALL PENNO(Z,N)

C  PENST(Z,N,M,K,L)ALMACENA Y RECUPERA LOS VECTORES DEL DISCO
C  DE ACUERDO CON LA OPCION L, EL ARGUMENTO ES UN VECTOR Z DE
C  DIMENSION N K EL ARCHIVO DEL DISCO QUE SERA EMPLEADO Y M
C  ES EL NUMERO DE REGISTRO

   12 CALL PENST (Z,N,100+I,K,3)
      A1=A1+F
   30 A2=A2-F

C       EN ESTA PARTE GRAFICAMOS LOS MODOS NORMALES DE VIBRACION
C  LA OPCION ES QUE PUEDEN SER GRAFICADOS CON ESTRELLAS Y UNIDOS
C  MANUALMENTE O GUARDADOS EN ALGUN REGISTRO PARA QUE DESPUES
C  SEAN UNIDOS AUTOMATICAMENTE
C
C  EN ESTA PARTE GUARDAMOS LOS EIGENVALORES EN EL REGISTRO 200
C  PARA DESPUES GRAFICARLOS POR MEDIO DEL PLOTTER EN EL PLANO
C  C2 Y C1
C
      DO 98 J=1,N
      WRITE (200'J)(X(J,K),K=1,41)
   98 CONTINUE
      WRITE(LO,352)
  352 FORMAT(1H1)
      DO 32 I=1,N
C
C         PENPG (Z,N,M,K,L) HACE UNA PAGINA DE GRAFICA DE LOS
C  EIGENVECTORES, Z ES EL VECTOR QUE CONTIENE LAS COMPONENTES
C  (NORMALIZADAS) DEL EIGENVECTOR DE DIMENSION N, M ES LO QUE
C  DESEAMOS SACAR, K ES EL NUMERO DE ARCHIVO EN QUE LOS PUNTOS
C  VAN HACER INTRODUCIDOS Y L ES LA OPCION
C
      CALL PENPG(Z,N,0,10,1)
      CALL PENPG(Z,N,0,10,2)
      CALL PENST(Z,N,100+I,41,4)
      DO 31 K=1,41
      CALL PENST (Z,N,100+I,K,5)
   31 CALL PENPG (Z,N,K,10,3)
   32 CALL PENPG (Z,N,I,10,5)
      CALL EXIT
      END

//FOR
*ONE WORD INTEGERS
*LIST ALL
C
C  SUBRUTINA PENGR GRAFICA LOS EIGENVALORES O FRECUENCIAS
C  DEL ESPECTRO POR, MEDIO DE LA IMPRESORA.
C
      SUBRUTINE PENGR(Z,W1,W2)
      DIMENSION  Z(1),III(120)
      COMMON     N,LI,LO
      S=100.0/(W2-W1)
      DO 11 I=1,120
   11 III(I)=16448
      DO 12 I=1,101,10
   12 III(I)=-14016
      L1=0
      IH=-3776
      II=256
      DO 27 I=1,N
      L=IFIX((-Z(I)-W1)*S+1)
      IF(L) 27,27,21
   21 IF(L-120) 22,22,27
   22 IF(L-L1)24,23,24
   24 L1=L
      III(L)=IH
      GO TO 26
   23 III(L)=-15292
   26 IH= IH+II
   27 CONTINUE
      WRITE  (LO),300) III
  300 FORMAT (1X,120A1)
      RETURN
      END

// FOR
*ONE WORD INTEGERS
*IOCS(1403 PRINTER,2501 READER)
*IOCS(DISK,PLOTTER,KEYBOARD,TYPEWRITER)
*LIST ALL
*NAME PENHL
C  *********************************************************
C
C                        APENDICE C
C
C                    PROGRAMA PRINCIPAL
C
C                         PENHL
C
C  *********************************************************
C
C  DESCRIPCION DEL PROGRAMA QUE GRAFICA LOS MODOS NORMALES DE
C  VIBRACION POR MEDIO DEL GRAFICADOR

      DIMENSION   X(501),Y(501)
      DIMENSION   EX(101),WY(101)
      DIMENSION   XL(501),YL(501)
      DIMENSION   XU(501),YU(501)
      COMMON      X0,Y0,X1,Y1,XS,YS,OX,OY,EP
      DEFINE FILE  10(57,120,U,K1)
      DEFINE FILE 101(41,96,U,K01)
      DEFINE FILE 102(41,96,U,K02)
      DEFINE FILE 103(41,96,U,K03)
      DEFINE FILE 104(41,96,U,K04)
      DEFINE FILE 105(41,96,U,K05)
      DEFINE FILE 106(41,96,U,K06)
      DEFINE FILE 107(41,96,U,K07)
      DEFINE FILE 108(41,96,U,K08)
      DEFINE FILE 109(41,96,U,K09)
      DEFINE FILE 110(41,96,U,K10)
      DEFINE FILE 111(41,96,U,K11)
      DEFINE FILE 112(41,96,U,K12)
      DEFINE FILE 113(41,96,U,K13)
      DEFINE FILE 114(41,96,U,K14)
      DEFINE FILE 115(41,96,U,K15)
      DEFINE FILE 116(41,96,U,K16)
      DEFINE FILE 117(41,96,U,K17)
      DEFINE FILE 118(41,96,U,K18)
      DEFINE FILE 119(41,96,U,K19)
      DEFINE FILE 120(41,96,U,K20)

      N=8
      HN=0.5*FLOAT(N)
      MD=501
      Y2=2.0
      Y1=-2.0
      X1=-5.0
      X2=5.0
      NX=N
      NC=41
      NX=MIN0(NX,101)
      NC=MIN0(NC,1O1)
      X0=-3.50
      Y0=-3.25
      XS=8.0/(X2-X1)
      YS=5.0/(Y2-Y1)
      EP=1.0E-3
      DX=-1.0/FLOAT(NC-1)
      DY= 1.0/FLOAT(NC-1)
      DO 10 I=1,NX
  10  FX(I)=FLOAT(I-1)-HN
      DO 40 K=1,N
      NU=0
      NL=0
      0X=0.0
      0Y=0.0
      CALL PHFVV(K)
      DO 30 I=1,NC
      K1=100+K
      READ (K1'I)(WY(J),J=1,NX)
      CALL VISUB (X,Y,J,MD,EX,WY,NX,XU,YU,NU)
      NU=J
      CALL VISCY (XU,X,NU)
      CALL VISCY (YU,Y,NU)
      CALL VISLB (X,Y,,J,MD,EX,WY,NX,XL,YL,NL)
      NL=J
      CALL VISCY (XL,X,NL)
      CALL VISCY (YL,Y,NL)
      0X=0X+DX
  30  0Y=0Y+DY
      CALL PHFMV
  40  CONTINUE
      CALL EXIT
      END

//FOR
*ONE WORD INTEGERS
*LIST ALL
C
C   PHFVV SUBROUTINE QUE HACE LOS MARCOS INTERIOR Y EXTERIOR 
C   PARA LAS GRAFICAS PONIENDO EL NUMERO DEL EIGENVECTOR 
C   CORRESPONDIENTE

      SUBROUTINE PHFVV(K)

      PI=3.1416
      CALL SCALF(9.8/11.,9.8/11.0,0.0,0.0)
      CALL FPLOT(2,0.0,11.0)
      CALL FPLOT(0,8,5,11.0)
      CALL FPLOT(0,8.5.0.0)
      CALL FPLOT(0,0.0,0.0)
      CALL FCHAR(0.39,2.0,0.07,0.07,-PI/2.0)
      WRITE(7,10)
  10  FORMAT('U.A.P. V.V.N')
      CALL FCHAR(0.53,2.0,0.07,0.07,-PI/2.0)
      WRITE(7,11)
  11  FORMAT('I.P.N  E.S.F.M')
      CALL FPLOT(-2,1.0,1.0)
      CALL FPLOT(0,1.0,10.0)
      CALL FPLOT(0,7.5,10.0)
      CALL FPLOT(0,7.5,1.0)
      CALL FPLOT(0,1.0,1.0)
      CALL FCHAR(7.64,9.0,0.08,0.08,-PI/2.0)
      WRITE(7,13)K
  13  FORMAT('MODO NORMAL ='I2)
      CALL FPLOT(1,4.25,5.5)
      CALL SCALF(9.8/11.,9.8/11.,0.0,0.0)
      RETURN
      END

//FORTRAN
*ONE WORD INTEGERS
*LIST ALL
C
C    PHFMV SUBROUTINE QUE DA OPCION PARA ESCOGER LA REGION DE LA
C    PROXIMA GRAFICA
C
      SUBROUTINE PHFMV
   10 FORMAT(' DAR EL CONTROL DE LA NUEVA PAGINA, COLOCAR EN ON ',//
     ='SWITCH 0 SI SE GRAFICO EN LA PRIMERA REGION ',//
     ='SWITCH 1 SI SE GRAFICO EN LA SEGUNDA REGION ',//
     ='SWITCH 2 SI SE GRAFICO EN LA TERCERA REGION ',//
   6  PAUSE
      DO 2 I=1,3
      J=I-1
      CALL DATSW(J,K)
      GO TO(3,2),K
    3 GO TO(4,4,5),I
    2 CONTINUE
      WRITE(1,11)
   11 FORMAT(//,'   AUN SIGO ESPERANDO ',//)
      GO TO 6
    4 CALL FPLOT(1,-4.25,5.5)
      GO TO 7
    5 CALL FPLOT(1,4.3,-27.5)
    7 CALL SCALF(1.0,1.0,0.0,0.0)
      RETURN
      END

//FOR
*IOCS(1403PRINTER.2501READER,PLOTTER)
*IOCS(TYPEWRITER,KEYBOARD,DISK)
*ONE WORD INTEGERS
*LIST ALL
*NAME
C
C ***************************************************************
C
C                            APENDICE D
C
C                         PROGRAMA PRINCIPAL
C
C                                PENCC
C
C ***************************************************************
C
C         DESCRIPCION DEL PROGRAMA QUE COMPRUEBA LOS RESULTADOS 
C  OBSERVADOS DE LOS MODOS NORMALES DE VIBRACION, GRAFICANDO LOS 
C  NUMEROS DE ONDA EN EL PLANO C1,C2, CORRESPONDIENTES A LAS
C  DIFERENTES FRECUENCIAS
C
      DIMENSION X(12,41)
      DEFINE FILE(200(12,82,U,IK)
      N=8
      L0=5
      F=.045
      A2=1.9
      A1=0.1
      XMG=1.4
      XMP=0.875
      Y=A1/A2
      RHO=XMP/XMG
      IM=1
      CALL PHF00 (L)
      CALL PHFVE(IM)
      CALL PHFRI (-1.5,-1.5,1)
      CALL PHFRI (1.5,11.5,2)
      CALL PHFRI (0.0,0.0,3)
      CALL PHRFI (0.0,0.0,4)
      CALL POINT (1)
      CALL PHFRI (1.0,1.0,3)
      CALL PHFRI (1.0,1.0,4)
      CALL POINT (1)
      CALL PHFRI (1.0,-1.0,3)
      CALL PHFRI (1.0,-1.0,4)
      CALL POINT (1)
      CALL PHFRI (-1.0,1.0,3)
      CALL PHFRI (-1.0,1.0,4)
      CALL POINT (1)
      CALL PHFRI (-1.0,-1.0,3)
      CALL PHFRI (-1.0,-1.0,4)
      CALL POINT (1)
      DO 19 J=1,N
      READ (200'J)(X(J,K),K=1,41)
   19 CONTINUE
      DO 10 I=1,N
      CALL PENCG (X(I,1)/A2,Y,RHO,Y1,X1)
      CALL PHFRI (X1,Y1,3)
      DO 11 J=1,41
      CALL PENCG (X(I,J)/A2,Y,RHO,YN,XN)
      CALL PHFRI (XN,YN,4)
      A1=A1+F
      A2=A2-F
   11 Y=A1/A2
      WRITE (LO,400)
  400 FORMAT (1X,//)
      A2=1.9
      A1=0.1
      Y=A1/A2
   10 CONTINUE
      CALL PHFEJ (L)
      CALL EXIT
      END

//FOR
*ONE WORD INTEGERS
*LIST ALL
C
C  PHFVE SUBROUTINE QUE HACE LOS MARCOS INTERIOR Y EXTERIOR PARA
C  LAS GRAFICAS PONIENDO EL NUMERO DEL EIGENVALOR POR GRAFICARSE
C  EN EL PLANO C1 C2
C
      SUBROUTINE PHFVE(IM)
      PI=3.1416
      CALL SCALF(9.8/11.,9.8/11.0,0.0,0.0)
      CALL FPLOT(2,0.0,11.0)
      CALL FPLOT(0,8.5,11.0)
      CALL FPLOT(0,8.5,0.0)
      CALL FPLOT(0,0.0,0.0)
      CALL FCHAR(0.39,2.0,0.07,0.07,-PI/2.0)
      WRITE(7.10)
   10 FORMAT('U.A.P  V.V.N')
      CALL FCHAR(0.53,2.0,0.07,0.07,-PI/2.0)
      WRITE(7,11)
   11 FORMAT('I.P.N   E.S.F.M')
      CALL FPLOT(-2,1.0,1.0)
      CALL FPLOT(0,1.0,10.0)
      CALL FPLOT(0,7.5,10.0)
      CALL FPLOT(0,7.5,1.0)
      CALL FPLOT(0,1.0,1.0)
      CALL FCHAR(8.14,9.0,0.08,0.8,-PI/2.0)
      WRITE(7,12)IM
   12 FORMAT('EIGENVALOR'I2)
      CALL FCHAR(7.78,9.0,0.08,0.08,-PI/2.0)
      WRITE(7,13)
   13 FORMAT('EN EL PLANO C1,C2')
      CALL FPLOT(1,4.25,5.5)
      CALL SCALF(9.8/11.,9.8/11.,0.0,0.0)
      RETURN
      END

//FOR
*ONE WORD INTEGERS
*LIST ALL
C  PENCG (Z1,Y,RHO,C1,C2) NOS DA LOS VALORES DE LAS COORDENADAS 
C  C1,C2 PARA DESPUES GRAFICARLAS POR MEDIO DEL GRAFICADOR, 
C  Z1=LAMBDA/A2,  Y=A1/A2  Y RHO ES LA RELACION DE 
C  MASAS=MASA CHICA/MASA GRANDE.
C
      SUBROUTINE PENCG  (Z1,Y,RHO,C1,C2)
      CRHO=SQRT(RHO)
      CRHO=CRHO + 1.0/CRHO
      B=CRHC*Z1+(Y+2.0)**2
      AC=4.0*(Z1*Z1+2.0*CRHO*Z1*(Y+1.)+2.0*((Y+2.0)**2-2.0))
      IF(B*B-AC)32,33,34
   32 SQ=SQRT(AC-B*B)
      C1=0.25*(B+SQ)
      C2=0.25*(B-SQ)
      WRITE(5,28)C1,C2
   28 FORMAT(1X,  ' C1P='F10.4, 3X,' C2P='F10.4)
      RETURN
   33 B=B/4.0
      C1=B
      C2=B
      WRITE(5,24)B,B
   24 FORMAT(1X, '  B = 'E14.6,3X, ' B = 'E14.6)
      RETURN
   34 SQ=SQRT(B*B-AC)
      C1=0.25*(B+SQ)
      C2=0.25*(B-SQ)
      WRITE(5,23)C1,C2
   23 FORMAT(1X,'  C1=  'F10.4,3X,' C2= 'F10.4)
      RETURN
      END


//FOR
*IOCS(1403 PRINTER,2501READER,DISK)
*ONE WORD INTEGERS
*LIST ALL
*NAME PENTA
C
C *************************************************************
C
C                            APENDICE E
C
C                        PROGRAMA PRINCIPAL
C
C                               PENTA
C
C *************************************************************
C
C  LA DESCRIPCION DE UNO DE LOS PROGRAMAS QUE SE EMPLEARON PARA
C  CALCULAREL ESPECTRO DE FRECUENCIAS Y LOS MODOS NORMALES DE
C  VIBRACION
C
C             PENTA ES EL PROGRAMA PRINCIPAL QUE NOS CALCULA LOS
C  EIGENVALORES Y EIGENVECTORES DE UNA MATRIZ PENTADIAGONAL A LA
C  CUAL SE LE PUEDEN HACER MODIFICACIONES EN LAS ESQUINAS DE SUS
C  DIAGONALES
C
C  INSTRUCCIONES DE ENTRADA QUE SIRVEN PARA DEFINIR ARREGLOS,
C   NOMBRES DE VARIABLES Y PARA DEFINIR ARREGLOS EN EL DISCO
C
      DIMENSION   X(12,41)
      DIMENSION   Z(32)
      DIMENSION   V(31),U(10,10)
      DIMENSION   G(10,10)
      COMMON      N,LI,L0
      DEFINE FILE 200(12,82,U,IK)
      DEFINE FILE  10(57,120,U,K1)
      DEFINE FILE 101(41,96,U,KO1)
      DEFINE FILE 102(41,96,U,K02)
      DEFINE FILE 103(41,96,U,K03)
      DEFINE FILE 104(41,96,U,K04)
      DEFINE FILE 105(41,96,U,K05)
      DEFINE FILE 106(41,96,U,K06)
      DEFINE FILE 107(41,96,U,K07)
      DEFINE FILE 108(41,96,U,K08)
      DEFINE FILE 109(41,96,U,K09)
      DEFINE FILE 110(41,96,U,K10)
      DEFINE FILE 111(41,96,U,K11)
      DEFINE FILE 112(41,96,U,K12)
      DEFINE FILE 113(41,95,U,K13)
      DEFINE FILE 114(41,96,U,K14)
      DEFINE FILE 115(41,96,U,K15)
      DEFINE FILE 116(41,96,U,K16)
      DEFINE FILE 117(41,96,U,K17)
      DEFINE FILE 118(41,96,U,K18)
      DEFINE FILE 119(41,96,U,K19)
      DEFINE FILE 120(41,96,U,K20)
C
C  INSTRUCCIONES DE ENTRADA PARA LEER LA DIMENSION (N) QUE
C  DESEAMOS ANALIZAR
C
      LI=8
      L0=5
      READ  (LI,20) N
   20 FORMAT(I2)
      IF(N) 2,2,3
    2 CALL EXIT
    3 WRITE   (L0,300) N
  300 FORMAT  ('1N='I2)
C
C  GENERACION DE LOS ELEMENTOS MATRICIALES .-LLENAMOS LA MATRIZ
C  TENIENDO EN CUENTA SU FORMA PENTADIAGONAL (DIAGONALES A,B,C,
C  D,E) LO CUAL NOS PERMITE UTILIZAR MENOS MEMORIA DE LA MAQUINA,
C  ESTA PARTE ES LA QUE GENERALMENTE DIFIERE DE MODELO A MODELO
C
      F=0.045
      XMG=1.4
      XMP=0.875
      A1=0.1
      A2=1.9
      A0=-2.0*(A1+A2)
      EPSIL=0.01
      DO 30 K=1,41
      X1=A1/SQRT(XMP*XMG)
      X2=A2/XMP
      X0=A0/XMP
      Y2=A2/XMG
      Y0=A0/XMG
      DO 97 I=1,N
      DO 97 J=1,N
   97 G(I,J)=0.0
      DO 10 I=1,N,2
   10 G(I,I)=X0
      N11=N-1
      DO 13 I=1,N11
      J=I+1
      G(I,J)=X1
   13 G(J,I)=G(I,J)
      N12=N-2
      DO 11 I=2,N,2
   11 G(I,I)=Y0
      DO 14 I=1,N12,2
      J=I+2
      G(I,J)=X2
   14 G(J,I)=G(I,J)
      D0 17 I=2,N12,2
      J=I+2
      G(I,J)=Y2
   17 G(J,I)=G(I,J)
      G(2,N)=Y2
      G(1,N)=X1
      G(1,N-1)=X2
      G(N-1,1)=G(1,N-1)
      G(N,2)=G(2,N)
      G(N,1)=G(1,N)
      CALL PENJA (G,EPSIL,V,U)
      D0 23 J=1,N
   23 X(J,K)=V(J)
C
C  PENGR (W,Z1,Z2)GRAFICA LOS EIGENVALORES POR MEDIO DE NUMEROS,
C  IMPRIMIENDO EL NUMERO DEL EIGENVALOR CORRESPONDIENTE Y Z1,Z2
C  SON LOS LIMITES DE DONDE SE QUIERE VER LA GRAFICA
C
      CALL PENGR (V,0.0,8.0)
C
C           CALCULO DE LOS EIGENVECTORES
C
      D0 18 J=1,N
      D0 12 I=1,N
   12 Z(I)=U(I,J)
C
C  PENNO NORMALIZA LAS PRIMERAS N COMPONENTES DEL VECTOR DE
C  ARGUMENTO Z
C
       CALL PENNO(Z,N)
C
C  PENST (Z,N,M,K,L)ALMACENA Y RECUPERA LOS VECTORES DEL DISCO
C  DE ACUERDO CON LA OPCION L, EL ARGUMENTO ES UN VECTOR Z DE
C  DIMENSION N, K EL ARCHIVO DEL DISCO QUE SERA EMPLEADO Y M
C  ES EL NUMERO DE REGISTRO
C
   18 CALL PENST (Z,N,100+J,K,3)
      A1=A1+F
   30 A2=A2-F
C
C      EN ESTA PARTE GRAFICAMOS LOS MODOS NORMALES DE VIBRACION
C  LA OPCION ES QUE PUEDEN SER GRAFICADOS CON ESTRELLAS Y UNIDOS
C  MANUALMENTE O GUARDADOS EN ALGUN REGISTRO PARA QUE DESPUES
C  SEAN UNIDOS AUTOMATICAMENTE
C
C  EN ESTA PARTE GUARDAMOS LOS EIGENVALORES EN EL REGISTRO 200
C  PARA DESPUES GRAFICARLOS POR MEDIO DEL PLOTTER EN EL PLANO
C  C2  Y  C1
C
      D0 98 J=1,N
      WRITE (200'J)(X(J,K),K=1,41)
   98 CONTINUE
      WRITE(L0,352)
  352 FORMAT(1H1)
      D0 32 I=1,N
C
C          PENPG (Z,N,M,K,L) HACE UNA PAGINA DE GRAFICA DE LOS
C   EIGENVECTORES, Z ES EL VECTOR QUE CONTIENE LAS COMPONENTES
C  (NORMALIZADAS) DEL EIGENVECTOR DE DIMENSION N,  M ES LO QUE
C   DESEAMOS SACAR, K ES EL NUMERO DE ARCHIVO EN QUE LOS PUNTOS
C   VAN HACER INTRODUCIDOS Y  L ES LA OPCION
C
      CALL PENPG(Z,N,O,10,1)
      CALL PENPG(Z,N,O,10,2)
      CALL PENST(Z,N,100+I,41,4)
      D0 31 K=1,41
      CALL PENST (Z,N,100+I,K,5)
   31 CALL PENPG (Z,N,K,10,3)
   31 CALL PENPG (Z,N,I,10,5)
      CALL EXIT
      END

//FOR
*ONE WORD INTEGERS
*LIST ALL
C
C  SUBROUTINA PENOR  ORDENA EN FORMA CRECIENTE CUALQUIER ARREGLO
C
      SUBROUTINE PENOR (X,Y,V)
      DIMENSION X(31),Y(31),V(10,10),H(10)
      COMMON      N,LI,L0
      D0 15 I=1,N
      XMIN=X(I)
      DO 16 J=I,N
      IF (XMIN-X(J))16,16,17
   17 P=XMIN
      XMIN=X(J)
      X(J)=P
      D0 10 L=1,N
      H(L)=V(L,I)
      V(L,I)=V(L,J)
   10 V(L,J)=H(L)
   16 CONTINUE
      Y(I)=XMIN
   15 CONTINUE
      RETURN
      END

//FOR
*ONE WORD INTEGERS
*LIST ALL
C
C  SUBROUTINA PENJA SIRVE PARA CALCULAR POR EL METODO DE JACOBI
C  LOS EIGENVALORES Y EIGENVECTORES DE LA MATRIZ DE MOVIMIENTO A
C
      SUBROTINE PENJA (A,EPSIL,L,V,U)
      DIMENSION A(10,10),B(10,10),C(10,10),R(10,10),RT(10,10)
      DIMENSION U1(10,10),U(10,10),V1(31),V(31)
      COMMON      N,LI,L0
      CALL MATUM(U)
   25 CALL MATCY(B,A)
      CALL MATDS(B,0)
      CALL MATAM(AM,L,M,B)
      IF(AM-EPSIL)40,40,41
   41 A1=B(L,M)
      A2=A(L,L)
      A3=A(M,L)
      A4=A(M,M)
      IF(A2-A4)20,20,21
   20 E=-(A2-A4)+SQRT((A2-A4)**2+A1**2)
      TAG=E/A1
      GO TO 22
   21 W=-(A2-A4)-SQRT(A2-A4)**2+A1**2)
      TAG=W/A1
   22 COS=1.0/SQRT(1.0+TAG**2)
      SEN=COS*TAG
      CALL MATUM(R)
      R(L,L)=COS
      R(L,M)=-SEN
      R(M,L)=SEN
      R(M,M)=COS
      CALL MATUM(RT)
      RT(L,L)=COS
      RT(L,M)=SEN
      RT(M,L)=-SEN
      RT(M,M)=COS
      CALL MATPR(C,RT,A)
      CALL MATPR(A,C,R)
      CALL MATCY (U1,U)
      CALL MATPR (U,U1,R)
      GO TO 25
   40 D0 60 I=1,N
   60 V1(I)=A(I,I)
      CALL PENQR (V1,V,U)
      RETURN
      END

Next: Referencias Up: . Previous: . Contents

Pedro Hernandez 2006-02-21