Obtención de la matriz de movimiento del modelo de la cadena diatómica

El siguiente paso es establecer el método que se usará para resolver este tipo de modelo de cadena.

Consideremos el modelo de la cadena diatómica compuesto de ``n'' partí culas con sus extremos fijos y las partículas que intervienen de dos clases de masas diferentes en forma alternada; numeraremos a las partículas por la sucesión $1, 2, 3, 4...N$, y los desplazamientos que sufran dichas partículas en relación a su posición de equilibrio lo denotaremos por $X_{1}, X_{2}$, . . . . . $X_{n}$, respectivamente; esquemáticamente tenemos:

Figura 3

REPRESENTACION DE UNA CADENA DIATOMICA CON ``N'' PARTICULAS

Al vibrar la cadena y suponiendo que la única fuerza que actua es la de interacción a segundos vecinos, es decir la partícula i-ésima sólo interaccionará con las partículas I-2, I-1 a la izquierda y I+1, I+2 a la derecha, siendo la interacción con las demás partículas igual a cero.

Puesto que en nuestro modelo es válida la ley de Hoke la fuerza resultante aplicada a la i-ésima partícula, obedece a la ecuación del tipo:

$$F_{i} = -K(X_{i}-X_{i-1})-K(X_{i}-X_{i+1})-K^{1}(X_{i}-X_{i-2})-K^{1}(X_{i}-X_{i+2})$$

$$= -K (X_{i-1} + X_{i+1} - 2 X_{i}) - K^{1} (X_{i+2} + X_{i-2} - 2X_{i})$$ (I-1 )

donde $X_{i-2}, X_{i-1}, X_{i+1}, X_{i+2}$ son los correspondientes desplazamientos de los vecinos más próximos y $K, K^1$ son las constantes que intervienen en el desplazamiento de la partícula I al interaccionar con sus primeros y segundos vecinos respectívamente.

De una manera análoga las fuerzas restantes sobre las partículas 1 y $N$ serán de la forma:

$$F_1 = K(X_2 - 2X_1) + K^1(X_3 - 2X_1)$$

$$F_N = K(X_{N-1} - 2 X_N) + K^1(X_{N-2} - 2X_N)$$

De las ecuaciones anteriores no podemos decir que (I-1), sea válida para todas las partículas, por lo que valiéndonos de un artificio que consiste en agregar dos partículas ficticias en cada extremo de la cadena, cuyos desplazamientos los consideramos iguales a cero, con la anterior suposición, las dos últimas ecuaciones tomarán la forma (I-1), y empleando un procedimiento análogo con las partículas 2 y N-1 la ecuación (I-1) será válida para todos los átomos de la cadena.

Expresando en otra forma la ecuación (I-1) que obedece a la segunda ley de Newton se tiene:

$$M_{i} \ddot{X}_{i} = K(X_{i-1}+X_{i+1}-2X_{i})+K^1(X_{i-2}+X_{i+2}-2 X_{i})$$

$$= K^{1}X_{i-2}+KX_{i-1}+2(-K-K^{1})X_{i}+KX_{i+1}+K^{1}X_{i+2}$$ (I-2 )

Aplicando (I-2) a todas las partículas de la cadena y simplificando los coeficientes de los desplazamientos obtenemos el siguiente: sistema de ecuaciones diferenciales de segundo orden, llamadas ecuaciones de movimiento. 1pt

$$\begin{array}{cccccccccccc} M_{1} \ddot{X}_{1} & = & A_{2}... ... + & A_{2} X_{N+1} & + & A_{2} X_{N+2} \nonumber \end{array}$$

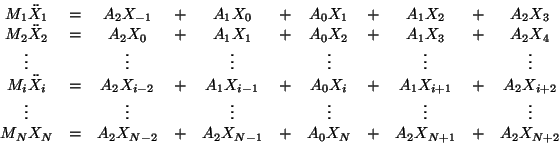donde $A_{1} = K, \quad A_{2} = K^1$ y $A_{0} = -2 (K + K^1)$
que expresada matricialmente adopta la siguiente forma:

$$M\ddot{X} = KX$$ (I-3 )

y en la que M y K son matrices de la forma:

$$M = \left [\begin{array}{cccccc} m_{1} & & & & & \\ & ... ... & & & & \ddots & \\ & & & & & m_{N} \end{array} \right ]$$

$$X = \left [ \begin{array}{c} x_{1} \\ x_{2} \\ \vdots \\ x_{i} \\ \vdots \\ x_{N} \\ \end{array} \right ]$$

$$K = \left [\begin{array}{cccccc} A_{0} & A_{1} & A_{2} & ... ...ots & \\ & & & A_{2} & A_{1} & A_{0} \end{array} \right ]$$

Despejando $\ddot{X}_{i}$ de las ecuaciones de movimiento (I-3) obtenemos un sistema que en forma matricial puede ser expresado como:

$$\ddot{X} = M^{-1} K X$$ (I-4 )

Una forma de resolver el sistema de ecuaciones diferenciales de segundo orden así presentado, es llegar a obtener los eigenvalores diagonalizando la matriz $Q$ que es el producto $KX$.

Si se observa detenidamente la matriz $Q$ se ve que no es simétrica, aunque no singular.

Ahora bién, empleando un método que permita que dicha matriz $Q$ adopte una forma simétrica facilitará muchos los cálculos al efectuar la diagonalización, lo cual se logrará en la siguiente forma.

Se multiplica por la izquierda a ambos miembros de la ecuación (I-5) por la matriz que denotaremos por $\sqrt{N}\ ^{-1}$ que el resultado de aplicar el operador
$\sqrt{\ \ \ }$ a cada uno de los elementos de la matriz diagonal M cuya estructura es:

$$\left [\begin{array}{cccccc} 1/\sqrt{m_{1}} & & & & & \\... ...ddots & \\ & & & & & 1/\sqrt{m_{N} } \end{array} \right ]$$

Además agregando la matriz identidad $\sqrt{M}$ $\sqrt{M}\ ^{-1}$ obtenemos una ecuación del tipo:

$$\sqrt{M} \ \ddot{X} = \sqrt{M}\ ^{-1} K \ \sqrt{M}\ ^{-1} \sqrt{M} \ X$$

y definiendo la transformación $Y = \sqrt{M} \ X$ la ecuación anterior toma la forma:

$$\ddot{Y} = A \ Y$$ (I-5 )

donde $\sqrt{M}\ ^{-1} \ K \ \sqrt{M}\ ^{-1}$ resulta ser simétrica y se le conoce con el nombre de matriz de movimiento o dinámica de la cadena diatómica.

La matriz $A$ en nuestro caso particular contiene implicitamente a las masa de las partículas de la cadena en una forma alternada que podemos denotar por ``m'' y ``M''. Presentando la siguiente forma:

$$A = \left [\begin{array}{cccccc} \frac{A_{0}}{m} & \frac{... ...rac{A_{1}}{\sqrt{mM}} & \frac{A_{0}}{m} \end{array} \right ]$$ (I-6 )