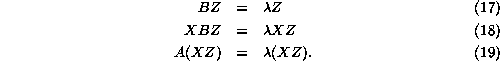Complementary graph

There is sufficient occasion to mention that certain links are not in a graph that it is convenient to construct a new graph composed entirely and exclusively of the missing links. The result is the complement of the given graph.

If it is not desired that all the links running in the wrong direction be included in the complement, the graph should be symmetrized before complementation.

At least when a graph contains single links without multiplicity, the connectivity matrix of the reversed graph is A-U, supposing that A is the matrix of the original graph and that U is a conformable square matrix, all of whose components are ones.

In terms of Eq. 3, for a homomorphism to preserve non-links (that is, the complementary graph) requires that

 

However, is a consequence of the definition of a function, that every point have one and only one image. Likewise holds when the function is onto and X lacks a zero column; together

 

The subscripts on U remind us that the dimension of each of the matrices may be different. Subtracting Eq. 13 from Eq. 14 and reversing the equality to compensate the sign produces

 

Comparison now yields the derivation of the assertion that equality in Eq. 3:

 

corresponds to the preservation of both links and non-links; note that X must be onto and not just into to get the result.

The strong homomorphism expressed in Eq. 16 guarantees that eigenvalues and eigenvectors of the image matrix belong to the source matrix as well: consider

   

Similar relations, in the opposite direction, hold for eigenrows.

---

Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx