Matrix representation
A rectangular matrix can represent a mapping between the nodes of one diagram and another; each column belonging to a node will have nonzero elements in the rows corresponding to the nodes mapping into it. In fact, the rows will be either orthogonal or identical, according to whether images are different or equal. The following relation is the matrix version of the mapping of a square to a digon shown in Figure 1:
0.4em
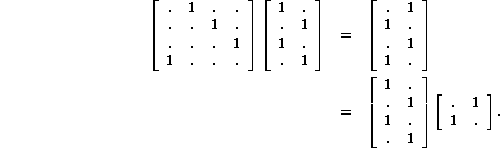
Likewise the mapping of the cartesian product shown in Figure 4 takes the form:
0.4em
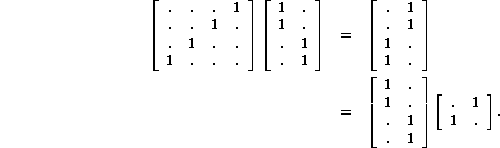
Link imaging is built into the matrix equation; the test of whether the mapping is a homomorphism is that the product matrix resemble the connectivity matrix of the image diagram, as determined by the respective arrangements of the nonzero elements. For example, if nodes a, b, and c of the square of Figure 1 were mapped into node a of the digon with node d mapping into node b, the equation above would become:
0.4em
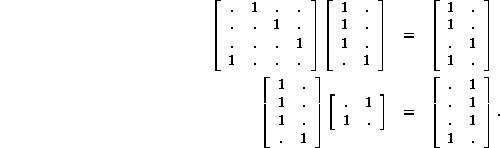
The discrepancy in the 
element of the products
is due to a linking to b in the square, then mapping to a in the
digon; alternatively it maps to a in the digon which can only link to the digon's b.
In mnemonic form, the matrix representation of a homomorphism is
normalized according to taste. Notice how the rows of the lefthand matrix scan the
nodes of the source diagram to see if there are any links to be followed. The right hand
side jumps directly to the destination to see whether there are any links that will
complete a commutative diagram. The inequality supposes that additional links may form
bridges. The combination definitely favors the 
version of the congruence relation.
In matrix form, the criterion for a homomorphism from the graph whose connectivity matrix is A to that whose matrix is B is for there to exist a conformable matrix X such that
In either of these formulations, inequality is sufficient to ensure the existence of links in the image set, but when equality prevails it means that there are no additional links in the image set. In other words, with equality both links and nonlinks are preserved.
It should be noted that inequality for nonnegative (indeed, arbitrary real) matrices is defined by requiring all corresponding pairs of matrix elements to satisfy the stated relationship. Generally, the matrix X of Eq. 3, consisting of zeroes and ones, rectangular if the orders differ, describes the mapping between the nodes of the two graphs. Note that numerical inequality of the matrix elements follows the sense of the mapping: homomorphisms increase monotonically; the connectivity matrix of the larger graph (the one left multiplied by X) has larger matrix elements, even though it may have fewer nodes.
Although Eq.3 is extremely elegant, it is also capable of great mischief. Equality is the preferred condition, since it implies conservation of both links and non-links; however the definition of graph ordering requires the additional inequality.
Sometimes matrices X fulfill Eq.3 without representing functions. A proper X must be row stochastic, otherwise nodes could have multiple images. If X were nevertheless column stochastic, the equation ought to be rearranged to take advantage of the implied inverse function.
The multiplicity of links often interferes with the interpretation of Eq. 3; to define homomorphism it is the pattern of zeroes which is relevant; matrix operations should be performed with boolean algebra followed by a numerical comparison, or else the nonzero elements should be normalized to ones before comparison. One is fortunate when ordinary algebra suffices for an entire calculation, which is the only way that additional conclusions regarding eigenvalues and eigenvectors will be valid.
Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx