We could then set up the matrix M for the eighteen symmetry classes
of the seven-cell rings. To obtain manageable indices, let us express each
binary class representative in decimal. Since these numbers are not
consecutive anyway, we might as well improve the appearance of M by
ordering the indices as they appear in maximal chains. Figure 
shows the evolutionary diagram together with its connectivity matrix
corresponding to a ring of length seven.
.2em
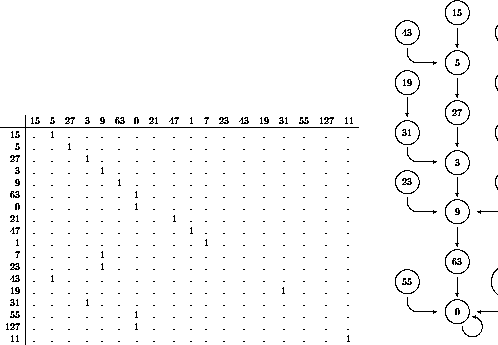
Figure: Evolution of a seven-cell ring under 
Rule 22.
There are seven classes without ancestors, corresponding to the zero columns. There are two static classes, represented by ones on the diagonal. Every class has just one successor, shown by the single one to be found in each row. Seven classes have unique ancestors; these are the ones with a single one in their column. Multiple ones within the same column mean multiple ancestors. All of this information can be obtained by inspection from any evolution matrix; much of it is discernible numerically by examining thr product of M with a vector all of whose components are ones.
The lengths of transients can also be read off from the matrix, as well as the lengths of cycles, but this information is harder to perceive. If, as has been done here, the row indices follow the evolutionary sequence insofar as possible, a chain of ones will be found on the superdiagonal of the submatrix corresponding to the cycle or transient. Otherwise the chain may be fairly well hidden among the other matrix elements.
Powers of the connectivity matrix, being less sparse, are often easier
to interpret because the remaining zeroes indicate disconnected groups
of nodes more clearly. In any event, the elements 
specify
the number of paths of length p running from node i to node j;
the diagonal elements therefore disclose the number of loops passing
through a given node. The trace in turn counts the total number of
loops; each loop is counted once for each of its nodes, but not for
multiple passes through the same node.
Some results which have been calculated for rings up to length 12 are
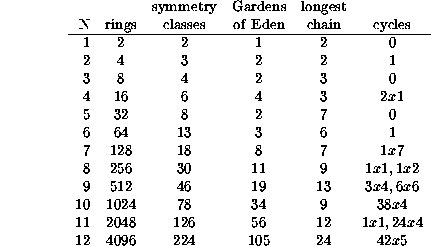
There are 
rings of length N, just the quantity of binary
numbers of that length; but the number of classes is a more complicated
group theoretical result[44, pp. 118-122,]:
In this formula, the symmetry operations g of the group G of
order 
have 
fixed points. When the symmetry is
rotational, the fixed points are sequences which repeat sooner than the
full length of the ring; for reflections they are palindromes.
For rotational classes, Golomb transforms this formula into an
expression involving Euler's function 
which counts divisors. The
main point of interest is that the number of classes grows
exponentially, although for longer rings it lags behind the number of
configurations by a factor which fluctuates around 2N, the size of
the dihedral group of rotations and reflections.
The remaining statistics have to be obtained on a case-by-case basis for each rule and each cycle length, although some rules admit special techniques --- for example if the rule of evolution is addition in a finite field. An extensive source of this kind of information is Wolfram's reprint collection[121], especially the tables of data in the appendix.