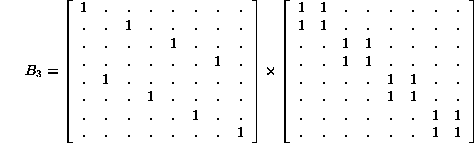
Expressing this equation in the form 
implicitly
defines the orthogonal permutation matrix P and a block diagonal U.
These matrices satisfy the equations 
, 
, where I is the unit matrix. Note that 
is a Kronecker
product, 
and that the following two
identities hold
Due to the symmetry of the matrix U, a slightly different factorization
is possible, in terms of a permutation matrix which we could call 
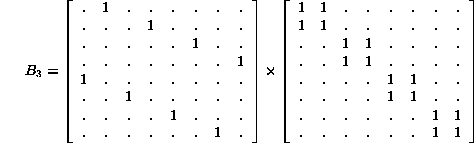
satisfies the equation 
but P and Q do
not commute. It is interesting to note that
Thus there are both factorizations and sum decompositions for the de Bruijn matrix, all readily obtained in a way that indicates that many more representations are possible, although the others would not be as symmetrical as the ones shown.
If we adopted a more formal definition of P and Q we would find
from which would follow
Writing the four terms of this sum according to their matrix elements,
we find (where 
is Kronecker's delta):
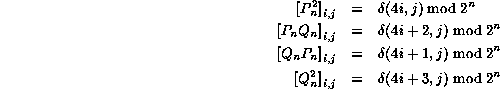
a representation which can readily be generalized for any power of B,
and also for any number of states per cell, 
In particular, the
form of both the minimal equation and the characteristic equation for
the de Bruijn matrices follows. Note that the congruence in these equations
is multiplicative, not additive, making 
congruent to 1, not 0.
The factorized form of the de Bruijn matrices can be used to obtain the determinants and inverses of their probabilistic generalization; since the strict de Bruijn matrices are singular their zero determinant can be derived in this way, but of course they have no inverses.