There are two ways that a de Bruijn diagram can be associated with the neighborhoods of a linear cellular automaton. The neighborhoods can be attributed to the nodes or to the links. The latter is the more compact representation; then the node between two links would describe the overlapping portion of the two neighborhoods. Any classification of neighborhoods immediately becomes a classification of the links. In searching for still lifes, we would discard all those links which did not stand for a neighborhood whose central cell evolved into itself.
If the remaining links formed chains, they would be chains which remained unchanged from one generation to the next. Unless they closed into loops however, they might dwindle away in each generation. If there were suitable loops, their lengths would determine the lengths of the ring automata in which they could be found. For example, chains of alternating ones and zeroes can only be found in rings of even length according to Rule 22, whereas the zero chain can exist in rings of any length.
Consequently loops often have to be extracted from larger fragments of de Bruijn diagrams, just as they have to be to get cycles from the evolutionary diagrams; in both cases the transients leading into the loops get discarded.
The formation of barriers between macrocells is one exception to the rule that only loops give interesting still lifes. The criterion for such a barrier is that the terminal nodes have a full complement of incoming or outgoing links according to the end of the chain which they occupy.
Another combination which often occurs is that a loop will be connected through a series of links to another loop, but that there is no return path. Thus some pattern may occupy the left side of an infinite chain, then undergo a transition into another pattern which occupies the right side of the chain. Such configurations were called fuses in Gardner's column and Wainwright's newsletter, and can exist in one dimension just as well as in two.
Nor are still lifes the only patterns which can be deduced from
de Bruijn diagrams. To obtain all the patterns of period two, it is
only necessary to iterate the evolutionary rule once and then look for
still lifes. This would transform a 
automaton into a 
automaton using a de Bruijn diagram of 4r stages, whose links would
be classified by their behaviour after two generations of evolution.
Similar considerations apply to periods of three or higher.
Any binary property at all of a neighborhood of cells can be reflected by its inclusion as a link in the de Bruijn diagram for neighborhoods of that length, and be extended to a larger region by pursuing chains throughout the diagram. Cells other than the central cell can repeat themselves, so that it is just as easy to search for shifting patterns as for periodic ones. Evolution into constant chains is likewise easy to test, and is helpful in determining the behaviour of backgrounds, particularly in automata with many states per cell.
.1em
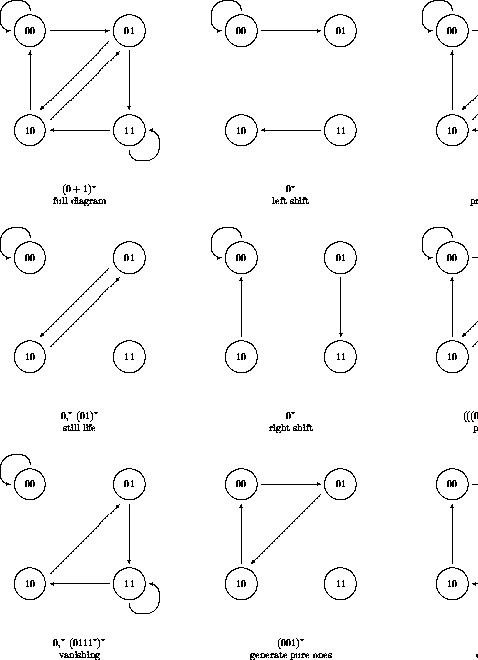
Figure: Simple properties of Rule 22 via de Bruijn diagrams.
Figure 
shows several examples; in fact configurations
possessing any of the attributes mentioned in Section , and
many more, can be read off by inspection, the 
de Bruijn diagram
being quite small.
Two less obvious properties can be mentioned. One is the search for
superluminal configurations. Quiescent automata are ones in which
there is a state q such that 
; when such a state
exists, it is generally assigned the value zero. Actually, especially
for automata which are not binary, there may be several quiescent
states, in which case only one of them would be labelled zero.
Quiescence simply means that a non-quiet cell cannot arise unless there
is another non-quiet cell in its neighborhood, which is to say,
``nearby.'' In quiescent automata information can propagate through a
quiet region at a maximum velocity equal to one radius per time step;
this velocity is picturesquely called the velocity of light.
A pattern can move faster than the velocity of light if it moves
through a region which is densely enough populated by non-quiet cells.
Superluminal configurations can always be found for any velocity, but
they may turn out to be so trivial as to be uninteresting. For example,
one may simultaneously be superluminal with a smaller velocity, or even
be a higher harmonic of a subluminal configuration. The argument is
that one can choose an arbitrary interval consisting of one
super-light-second plus half the width of the neighborhood. Say its
length is 
. Anything beyond this interval is fixed by the
combination of evolution and shifting. Of course, the shifted image
which emerges does not have to be part of the original interval, but
there is not much else that it can be because there are only 
intervals and 
images after g generations. So, there has
to be some interval which generates a recurrent pattern.
Idempotent rules lead to a particularly restrictive type of behaviour, but not all rules are idempotent. Still, one of the boolean questions which can be asked of second generation evolution is whether
and consequently whether a given rule admits any configurations which have an idempotent evolution even if all of them do not.