Conceptually superluminal configurations may be somewhat easier to
describe than those of lower velocity. For convenience, consider a
configuration, which is supposed to have a single phase which
shifts by a distance of 2 in each generation. Its evolution would have
the symbolic form
From this it is evident that a, b, and c are arbitrary, but that necessarily
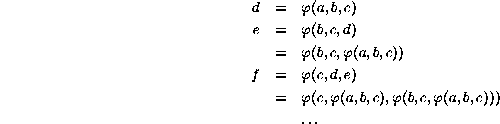
The point is that any seed sequence a, b, c determines the entire
sequence of cells from some point on, but only eight different binary
sequences of three cells are possible. The original seed need not
repeat itself, but some seed must repeat within at least eight cells.
Thus only eight strings need to be examined to ascertain all the
possible 
configurations; for Rule 22 we would find:
These configurations are not very interesting, because they all have simpler descriptions; but they all fulfill the technical description, and are moreover the only configurations which do so.
If one wanted to find 
configurations, the seed would have
length 4, and in general a 
configuration would have a seed of
length p+d and the superluminal configuration would have length less
than 
and have to be manifest within that many cycles of
iteration of the above procedure.
The following superluminal configurations (single phase, shift no longer than 12) exist for Rule 22:
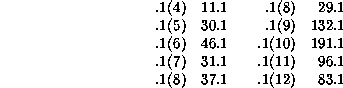
Subluminal configurations can be found by the same procedure, but since the displaced seed overlaps its own neighborhood, consistency requirements must be met. Thus superluminal configurations always exist even if they are degenerate or trivial, but subluminal configurations may fail the additional requirement. In any event, the de Bruijn diagram yields a more systematic procedure for all configurations, and the foregoing discussion is mainly useful an an existence theorem.