Whereas the diagram for the cycles of a linear cellular automaton is a collection of
``trees rooted in cycles,'' its periods are obtained from the de Bruijn diagram which
consists of an enormous number of cycles, all interlacing. Still, the length of a ring
with a given period is limited by the number of nodes in its de Bruijn diagram, which
after g generations is 
For one-generation
properties of a (2,1) automaton this number is 4. This means that any still life must be
evident in a ring whose length is no longer than 4, and that if there is a still life in a
longer ring, it must contain repeated segments whose length is no longer than 4.
There is only one loop of length 4 in a 2-stage binary de Bruijn diagram, formed by the sequence 0011; to require it to represent a still life makes the following demands on the transition rule:
Thus four neighborhoods have their evolution prescribed and for the other four it is
arbitrary. For the maximum variety, a, b, c, and d should be chosen opposite
to the central cell, yielding Rule 105, but there are altogether sixteen rules for which
the sequence 
is a still life. Of course, there
may be additional still lifes besides the one which was stipulated; for example if d
were chosen to be zero in this example, any number of additional zeroes could be inserted
into the sequence besides the two shown, and we would have Rule 104. Then 
would also be a still life. At the points where
additional zeroes can be inserted, there is no restriction on the exact number.
It is harder to survey the possible periods for a rule than the possible cycles because the lengths of the configurations that have to be checked grow twice as fast with increasing period as with increasing cycle length; thus if it is feasible to survey all cycles up to length 30, the corresponding limit for periods is 15. Furthermore, the diagram for cycles has only simple loops, whereas the period diagrams can have multiple loops, whose branching is somewhat harder to describe.
Shifting configurations are just as easy to determine as are the periodic
configurations; let the notation 
denote a
configuration which has period P with p phases after which time it has
shifted d cells to the left (a negative d signifies a right shift, which
only need be catalogued separately for non-symmetric rules). Reflective configurations of
the form 
can be found among the 
configurations, the calculation required to detect
them being the same in either case.
Actually it is better not to specify to specify the period, since it will depend somewhat on the length N of the ring in which it occurs. That is, if d does not divide N, the pattern may have to make several circuits of the ring before repeating itself, and
The smaller subluminal periods for Rule 22 have been determined; they include the following up through five generations:
2 generations :
, 
* 3 generations :
Figure 
4 generations :
and evolutes 
Figure 
5 g:
and evolutes 
.1em
Figure: Configurations satisfying .3(2) for Rule 22.
.1em
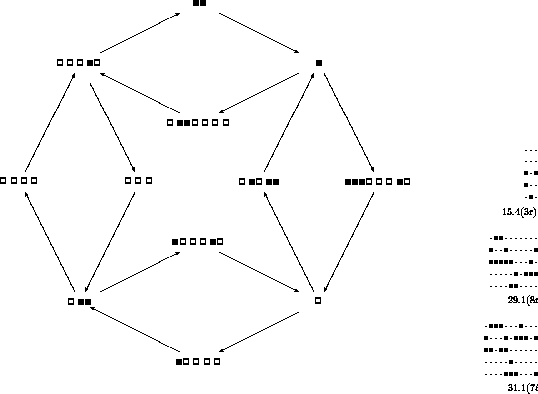
Figure: Configurations satisfying .4(3) for Rule 22.
The unshifted period six is interesting for a wide variety of cycles, all of whose
lengths are multiples of ten, situated as vertical faces on the hexagonal prism of Figure .
Of course the table continues indefinitely; shifting configurations of period six exist,
not to mention longer periods. Taking into account additional shifting and longer periods
tends to produce diagrams of increasing complexity, but three classes of diagram are
already apparent in the results shown here.
.1em
Figure: Configurations satisfying .6(0) for Rule 22.
First, there are simple cycles which evolve by shifting (including still lifes with zero shift); a single diagram serves all generations.
Next, there are diagrams, such as the .4(0) or .5(0) families, in which succeeding generations are described by distinct components of a disconnected diagram, although symmetric images of the first (and subsequent) generations may be encountered before the full period closes.
The third class, typified by the .4(3) configurations of Figure
or the .6(0) configurations of Figure , combines several different phases
within a single generation, producing a much more intricate single component diagram.
The .5(0) configurations arise from a single pair of cells embedded in a torus; two gaps separate them of which one always has length 4, the other may have length 5, 6, or 7. Altogether the cycle length may be 11, 12, or 13; longer configurations arise from joining the triplets in sequence.
By contrast, the .4(0) configurations also feature a live cell pair, but this time the short gap can have length 1, 2, or 3 while the long gap's length can be 5, 6, or 7; this time an ennead whose members can be sequenced.
In summary, the de Bruijn diagram determines sequences of neighborhoods, and therefore cyclic or infinite configurations which meet some requirement which can be placed on its links. Cyclic configurations follow from the loops inherent in the diagram, but aperiodic configurations also exist; these can arise in two ways.
If there are two loops with a one-way connection between them, such as can be seen in
Figure describing .3(2) configurations, a transition
between the two loops can be made at some point. The result in some cases has been called
a ``fuse,'' a left hand field arises which is different from the right hand field; the
boundary between them may be moving or static. To make a good fuse, the field from which
the boundary retreats should be quiescent.
If two loops are mutually connected, the transition back and forth can be made many times; imagine that the choice is made to correspond to the binary expansion of an irrational number to obtain an aperiodic configuration. The greater the variety of loops in the diagram, the greater the variety of configurations, but a connected pair is enough for aperiodicity.