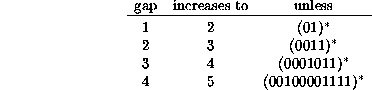
In the course of obtaining all the cycles of length up to N=34 for Rule 22, rings of cells were examined in such an order that those with more leading zeroes were examined first. Moreover, rings were discarded if, in the course of evolution, a ring appeared which might have been used earlier as a starting point, or was equivalent to such a ring by some symmetry operation. In effect, that meant if a ring evolved which contained a string with more zeroes than there were leading zeroes in the original ring, the analysis was halted and the next case considered.
It was quickly observed and proved that when a single leading zero was encountered, only one cycle was going to be discovered --- the still life if the length of the ring was even. Likewise, two leading zeroes would only lead to the ring of period two, and then only when the length of the ring was a multiple of four. If we say that a sequence of m zeroes (presumably bounded by ones at both ends) is a gap of length m, then the conditions in the following table were observed
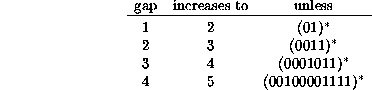
A conjecture that the only exceptions to gap 5 were the configurations of period 4 and period 6 was made, but proved intractable to verify. Essentially the conclusion was drawn that there would always be some phase of a cycle with a larger gap than a certain value unless the ring were of a particular form, generally of low period, in which the given gap was conserved.
These observations had practical importance because the search for cycles could be stopped when the leading gap got to be small enough. The search time doubled each time the leading gap was decreased by one, so that it was worthwhile to stop with the largest possible leading gap.
By the use of the de Bruijn diagram, the low order gap theorems can be derived; the procedure is applicable to any rule in any automaton. It is convenient to change the point of view of the theorems slightly. Rather than worry about ``gaps increasing,'' the question could be: What strings of cells do not evolve into gap m? This property is just one of many predicates which could be used to select subdiagrams from a de Bruijn diagram. For example, which strings of length three do not evolve into zero? Or, which strings of length four do not evolve into 00?
Since a small gap is contained in a larger one (gaps without worrying about boundaries), it must mean that only strictly smaller gaps can occur when a given gap is excluded from the next generation. Rings from which such gaps are excluded can only be made up from surviving loops in t de Bruijn diagram, and hence are even limited in their maximum length.
The simple exclusion of gaps from the second generation does not mean that the gaps were not present in the first generation, or that they might not appear in the third or subsequent generation. So, drop them from the first generation as well, leaving a finite set of candidates whose periods must be determined and which must be followed through their full cycle of evolution to see whether overly large gaps occur at some stage.
.1em
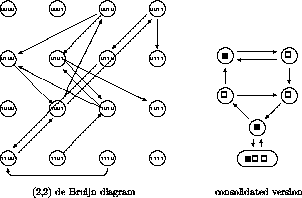
Figure: (2,2) de Bruijn diagram excluding 000 in first and second
generations.
Figure 
shows the process applied to Rule 22 for gap 3; using
the table of Section all links are excluded which contain
three consecutive zeroes in either the first or the second generation;
consolidating the results shows that either an additional generation
should have been considered (resulting in a larger starting diagram) or
some of the known counterimages of three zeroes should also have been
dropped (a rather ad hoc procedure).
The elimination of a gap from a sequence is similar to the construction
of Cantor's set, wherein the digit `1' is excluded from triadic
decimals constructed from the digits 
; but clearly
additional and fancier exclusions are possible. The difference lies in
extending the exclusion to several, and possibly all, generations; the
latter requires skill, persistence, and luck.
Carrying a diagram through additional generations generally reduces the
number of configurations which are admissible; the triangular bridge
lying between the cycles 
and 
disappears in the next
generation, leaving results which are provably applicable to all future
generations. The process works well because these cycles lack ancestors
other than themselves; but it is another matter to arrive at gap 5
which can be found in all Rule 22's period four configurations, all of
which have large numbers of ancestors with small gaps.
Useful results have been obtained for practically important cases with small gaps, but the theorems are slightly more complicated if aperiodic configurations are included: there are some interesting ``black hole'' states. Also to be borne in mind is the fact that for symmetrical rules such as Rule 22, symmetric images of exceptions are also exceptions, as we have tacitly assumed.
