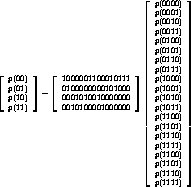
Figure: Two-block probabilities summed from four-block probabilities.
The motivation for working with block probabilities rather than cell probabilities is the hope that a better agreement with empirical observations can be obtained, supposing that up to some point longer blocks can better account for correlations between cells than short blocks can. Nevertheless, the empirical quantity which is usually calculated is the probability of individual cells. Sometimes variances or pair probabilities may also be calculated, but it is the density of cells which is the primary concern.

Figure: Two-block probabilities summed from four-block probabilities.
Cell density can be inferred from block probabilities by summing up the
probabilities of blocks in various ways, all of which are guaranteed to
give consistent results by virtue of the Kolmogorov consistency
conditions. It is thus worthwhile to investigate whether the iterative
solution of the local field theory equations conserves the consistency
conditions. We have shown that if the definition of ![]() -block
probabilities in terms of n-block probabilities is consistent, the
definitions for all shorter blocks will also be consistent. Thus it
suffices to show that one cycle of iteration conserves consistency at
the the highest level---the one which is anyway involved in defining
the denominators for
-block
probabilities in terms of n-block probabilities is consistent, the
definitions for all shorter blocks will also be consistent. Thus it
suffices to show that one cycle of iteration conserves consistency at
the the highest level---the one which is anyway involved in defining
the denominators for ![]() .
.
Wilbur et.al. included a proof in their article, so the only practical question remaining is one of stability---whether numerical errors arising during the course of an iterative solution of the equations could prejudice the consistency of the results.
It is in any event instructive to write the field equations in a very
extended explicit matrix form, shown here for 2-blocks evolving by Rule
22. We begin with equations (set aside in Figure ![]() due to their
bulk) expressing the probability of a block as the sum of the
probabilities of its possible ancestors.
due to their
bulk) expressing the probability of a block as the sum of the
probabilities of its possible ancestors.
Either Wilbur et.al.
's theory or Gutowitz et.al.
's equations written in Hartree-Fock form
estimate the probability of each 4-block ancestor in terms of the
probabilities of the 1- and 2-block segments into which the ancestor
can be decomposed. The matrix form of this estimate, in which the
precursor of the de Bruijn format is quite apparent, is shown in
Figure ![]() .
.
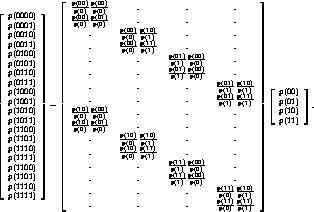
Figure: Four-block probabilities estimated from two-block
probabilities.
Consolidating these two equations produces a ![]() matrix of
coefficients
matrix of
coefficients
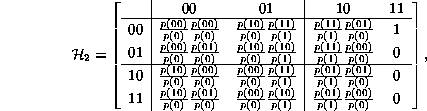
in which it can be verified by inspection that ![]() is consistently
defined by either
is consistently
defined by either ![]() or by
or by ![]() or that
equivalently
or that
equivalently ![]() on the right hand side implies the same
relation for the new values on the left hand side of the equation.
on the right hand side implies the same
relation for the new values on the left hand side of the equation.
It is easier to give the general proof in symbolic form, having first written the field equations in terms of the merged product:
![]()
If it is intended to write Q=AB so as to obtain
![]()
we need to know that
![]()
If ![]() is incorporated into X we introduce W
is incorporated into X we introduce W
![]()
and note that
![]()
so that
![]()
Since an entirely symmetrical expression results when Q is factored
into Q=BC, comparing the two establishes the consistency of ![]() after iteration, supposing that it was consistent before. The essential
points in the proof are, first, that running through all initial
letters in the sum for
after iteration, supposing that it was consistent before. The essential
points in the proof are, first, that running through all initial
letters in the sum for ![]() guarantees a traversal of all the initial
letters in the ancestors, and second, that the denominators in the
probabilities are cancelled by the sums in the numerators as a
consequence of the consistency hypothesis.
guarantees a traversal of all the initial
letters in the ancestors, and second, that the denominators in the
probabilities are cancelled by the sums in the numerators as a
consequence of the consistency hypothesis.