![]()
Un AC lineal es un sistema dinámico que evoluciona en tiempo y espacio discretos. El
espacio de acción del AC lineal es un arreglo lineal, en donde cada casilla se llama
célula y el valor de cada célula se toma de un conjunto finito E de valores
llamados estados y k es la cantidad de elementos que pertenecen al conjunto E
.
El conjunto de todas las células en el arreglo forman el estado global del AC,
también es llamada la configuración espacial y denotaremos con la letra G al
conjunto de las configuraciones globales de un AC.
Ahora, dada una configuración global

en el tiempo t , una regla de evolución genera una nueva configuración

asignando estados a todas las células de manera síncrona en base a los estados de una
secuencia finita de células contiguas llamada vecindad en la configuración ct .
Llamamos longitud de la vecindad al número de células que están implicadas en la
asignación del valor de la célula central en la siguiente generación. La longitud de la
vecindad está dada por n=2r+1 , donde r es la cantidad de células a la
derecha (o a la izquierda) de la célula en transición.
El arreglo en el cual el AC lineal está definido, puede ser un conjunto de m celdas colocadas en forma de anillo, es decir que después de la última celda x_m , sigue la primera

donde

o bien como un arreglo semi infinito por la derecha o infinito por ambos lados. Si es
el primer caso, denotaremos el conjunto de celdas dispuestas en forma de anillo por G_m
, si es infinito por la derecha G^+ , si es infinito por la izquierda G^- y
si es infinito por ambos lados G simplemente.
Hay aún otra forma de tratar los autómatas celulares lineales, y es considerar un
espacio finito por ambos lados de n células G_m , pero en vez de tratarse
de un anillo, es tratarlo de manera lineal, donde la última célula no es vecina de la
primera. En este caso en cada evolución de AC lineal el espacio de configuraciones
globales se reduce.
Una función global X transforma una configuración global en otra aplicando una regla de transición local f_X (que asigna un estado a una célula en base a los estados de las células en una vecindad alrededor de la célula en transición), la función global X está definida como una transformación del mismo arreglo unidimensional

y la función de transición o regla de evolución local
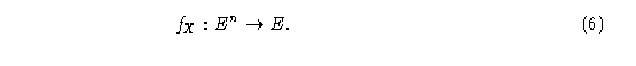
Podemos indicar con f también a la regla de evolución local f_X
queriendo decir con esto que a la secuencia s afectada por X se le aplica la
regla de evolución f_X a cada vecindad que se pueda formar.
Las reglas de evolución para AC lineales de 2 estados que cumplen
y todos los estados están representados en la imágen de la función, tienen propiedades determinantes por la izquierda. Y tienen propiedades determinantes por la derecha las reglas de evolución que cumplen con:
Y también todos los estados están representados en la imágen de la regla de
evolución. Definiendo la función de manera explícita, tenemos la tabla 1 para un AC
lineal (2,1) con propiedades de izquierda, y la tabla 2 para un AC lineal (2,1) con
propiedades de derecha.
Regla de evolución para AC con propiedades de izquierda:
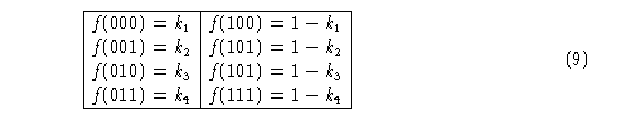
Regla de evolución para AC con propiedades de derecha:
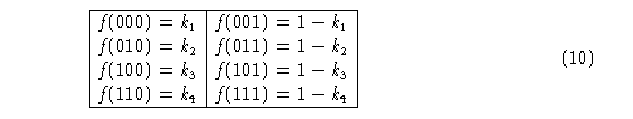
![]()