![]()
Sea (k,r) un AC con longitud de vecindad n=2r+1 y un conjunto de k estados. La gráfica de la función f denotada por
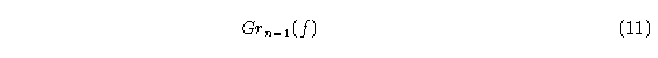
El conjunto de vértices está formado por todas las secuencias binarias

Las aristas son líneas dirigidas de un vértice i a otro vértice j. Existe una arista dirigida e_(ij) saliendo del vértice i y conectando con el vértice j si existe una secuencia
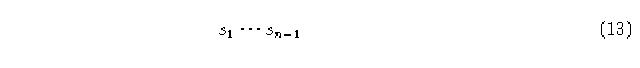
tal que
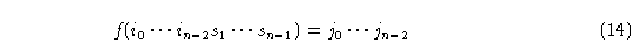
para AC lineales con propiedades de izquierda, para AC lineales con propiedades de derecha, tenemos de manera similar:
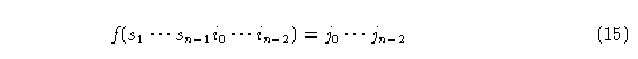
En esta gráfica se permiten aristas repetidas y ciclos de longitud 1. Las aristas de
la gráfica pueden estar etiquetadas con la secuencia de dígitos que cumplen la
condición antes mencionada.
La matriz de adyacencia de esta gráfica, está denotada por
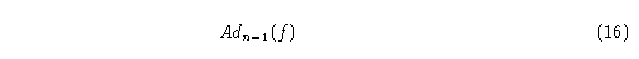
y se llama también la matriz básica de f. Si todas las entradas a_(ij)
de la matriz básica de la función tienen valor 1, entonces la gráfica de la función es
una gráfica completamente conectada, y quiere decir que podemos alcanzar cualquier
vértice desde cualquier vértice en una generación.
Teorema 1. Si f es una regla de evolución como la definida como en (1) o en (2) para un AC (2,1).

tiene

y

en cada vértice.
![]()
es la valencia de salida de cada nodo y
![]()
la valencia de entrada en cada nodo.
Demostración.- Si estamos hablando de un AC (2,1) y su regla de evolución es como la que se muestra en la tabla 1 observamos que los nodos de la gráfica de la función

tienen 2 dígitos binarios, los cuales son 00, 01, 10 y 11. Sea
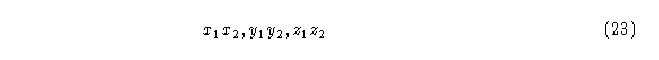
cualquier secuencia de este tipo;
![]()
representa la secuencia que etiqueta al nodo i de salida de una arista e_(ij),

representa la secuencia de dígitos binarios que etiqueta al nodo de llegada de la arista e_(ij). Entonces para que exista una arista del nodo

al nodo

debemos encontrar una secuencia
![]()
tal que
![]()
aplicando la regla de evolución a cada vecindad. Con este tipo de secuencias

podemos tener hasta 16 diferentes, y todas ellas definen una secuencia de 2 dígitos,
porque la regla de evolución considera todos los casos.
Ahora tenemos 16 ligas en la gráfica. Podemos dividir el problema en dos casos primero
demostraremos que la valencia de salida de cada nodo es 4. Después demostraremos que la
valencia de entrada a cada nodo es 4:
Caso 1 La valencia de salida de cada nodo. En este caso, estamos averiguando cuantas configuraciones cumplen con
![]()
donde
![]()
representan cualquier configuración de dos dígitos binarios que permanece constante. Para generar a z_1 hay solamente 2 posibilidades de lograrlo ya que c_1 y c_2 permanecen sin cambio. Para formar a z_2 hay 4 maneras ya que c_2 permanece sin cambio en la configuración
![]()
Como
![]()
es una configuración común en las configuraciones para formar
![]()
y dado que
![]()
es fijo solamente se pueden formar

a partir de 4 configuraciones. Esta es la valencia de salida de cada nodo.
Caso 2 La valencia de entrada a cada nodo. Podemos replantear el problema preguntando cuantas configuraciones resuelven
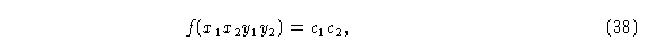
Para generar c_1 hay 8 configuraciones posibles de

y para formar c_2 también hay 8 configuraciones de

Pero dado que la regla de evolución cumple con (1) y tienen la forma de la tabla 1, entonces solamente hay 4 configuraciones para c_1 y 4 para c_2. Ahora,

son una secuencia que es común a las 8 configuraciones que forman

y solamente hay 4 combinaciones de

para formarlas, por lo que hay 4 secuencias

que bajo la función global X generan la secuencia

la cual es la valencia de salida. q.e.d.
Observaciones.- Si f es una regla de evolución como la definida como en (1) o en (2) para un AC (2,1).
![]()
tiene las siguientes características:
a) La suma de las entradas de cualquier renglón o columna es igual a 4; que es la
valencia de cada nodo.
b) Para cada entrada a_(ij) de
![]()
a_(ij) = a_(gh), donde
![]() y
y 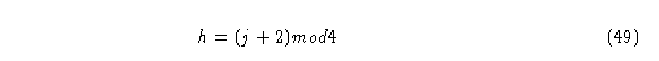
cuando la regla de evolución es del tipo (7).
Nota Cuando i o j son igual a 2, entonces g y h son igual a 0, pero como 4 está
en la misma clase de equivalencia de 0, entonces podemos decir que 4 mod 4 = 4. Esto es
con el fin de que el índice concuerde con la manera tradicional de etiquetar las filas y
las columnas en una matriz.
Ejemplo Sea f el AC (2,1) Regla de evolución 180 de acuerdo al criterio
de Wolfram [5].
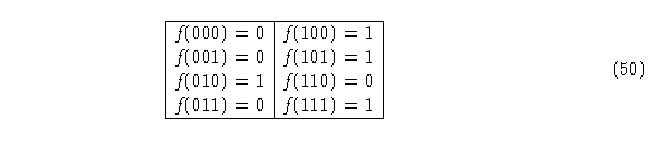
Configuraciones de 4 dígitos y su resultado bajo X
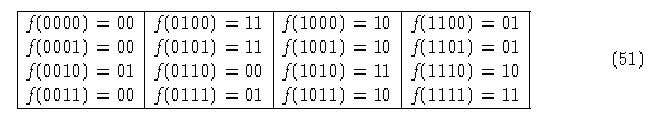
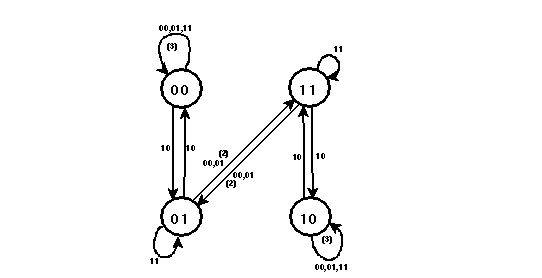
Figura 1: Gráfica de la función global Gr_2(f) del AC lineal
(2,1) Regla 180
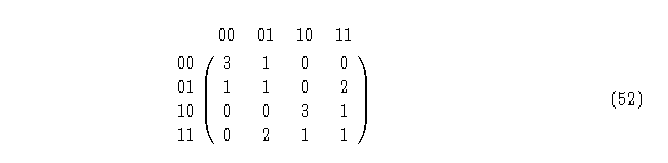
Matriz básica Ad_2(f), AC lineal(2,1) Regla 180.
La gráfica Gr_2(f) de la función es la que se muestra en la figura 1.
Esta gráfica y esta matriz nos pueden servir para saber cuándo una regla de evolución tiene o no Jardín de Edén (JE), es decir, determinar para una regla de evolución f el subconjunto
![]()
con todas las configuraciones que no tienen preimagen. Definimos GE(f) como

En el siguiente apartado, estudiaremos una manera de encontrar una preimagen de una
secuencia de estados. Y podremos encontrar todas las posibles configuraciones que son
preimagen de una secuencia dada y asi determinar si es o no un JE.
![]()