En la siguiente tabla se muestran algunos resultados usando reglas de evolución definidas sobre autómatas celulares lineales de k=2 estados y un radio de vecindad r=1:
En la columna dedicada al exponente característico de Liapunov, en algunos casos, se muestran los exponentes ![]() y
y ![]() separados por un guión. En ese orden.
separados por un guión. En ese orden.
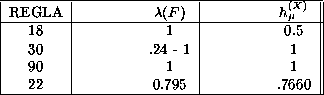
Un listado de las reglas de evolución para los autómatas celulares (2,1) se encuentra en [5]

Figura 7: Fragmento de la evolución del autómata celular definido por la regla totalística 33, en un espacio de 2 estados y un radio de vecindad 4

Figura8 : Mapa de retorno que señala el comportamiento colectivo no trivial mostrado por el autómata R33 totalística, haciendo un levantamiento a 4 dimensiones con la vecindad de von Neumman e iterando 250 veces
En la tabla que a continuación se muestra aparecen los resultados correspondientes a la regla 33 totalística definida sobre los autómatas celulares lineales de k=2 estados y r=4. Se ha escogido esta regla dado su comportamiento colectivo no trivial [11] [12] ver la figura 8.
![]()
Los resultados obtenidos son razonables al ver la evolución del autómata, que se muestra en la figura 7, primero, el exponente característico de Liapunov es justificado notoriamente al observar los patrones crecientes a cada evolución. Con lo que se concluye que la regla tiene un alto grado de caos.
Por otro lado, la medida de entropía es baja ya que como también se observa en la evolución, es más probable que sólo se generen secuencias de estados iguales de tamaño variable, y es casi imposible que aparezca una secuencia de tamaño 9 (el tamaño de la vecindad) con células de ambos estados, pero intercaladas en toda la vecindad, es decir la secuencia ``101010101'' tiene una probabilidad muy baja de ocurrir, es posible que unicamente aparezca como secuencia inicial.