La evolución de los autómatas celulares nos dan características básicas del comportamiento que tiene determinada regla a través del tiempo. Sea d la dimensión del autómata celular, i el sitio que ocupa cada célula dentro de la lattice, t el tiempo, 
el número de vecinos, 
la vecindad isotrópica (es decir, existen igual número de vecinos simétricos) y 
la concentración instantanea de 1's dentro de la lattice.
Tenemos una lattice y una vecindad de tamaño 
, para un autómata binario, es decir, dos estados ``0" y ``1".
Figura 3: Lattices de tamaño N
Definimos una regla totalística para un autómata celular de orden 
como:
donde la suma de los estados de una vecindad dada, debe tener un valor entero que representa todas las combinaciones posibles (vecindades equivalentes) que tengan ese mismo valor.
Tales reglas están definidas por un conjunto S de 
posibles transiciones de la regla totalística tal que 
, donde 
nos determinará todas aquellas vecindades que mapean en uno, especificadas por el conjunto S. Por lo que definimos:
Pr
| 
donde 
es el estado en el sitio i en el tiempo t y 
la configuración de la vecindad en el sitio i y el tiempo t para toda 
.
La mayoría de las reglas en estudio son totalísticas pues el número total de vecindades a análizar es considerablemente grande. Se define un estado absorbente dado por: 
. La última restricción considera sólo las reglas del conjunto definidas por la sucesión 
, determinada por el intervalo 
tal que:
donde el intervalo determina las vecindades que mapean al estado uno y las vecindades restantes al estado cero.
Esta restricción es parecida a la estructura que maneja Life [2]. Si una vecindad tiene poca población 
su célula central muere, esto es el estado absorbente. Si hay una sobrepoblación si 
ocurre lo mismo. Una célula sobrevive si posee una densidad apropiada.
Estos mapeos son realizados sobre las vecindades de John von Neumann [1] y Edward F. Moore [9] como se muestra en la Figura 4, respectivamente.
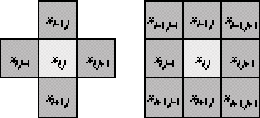
Figura 4: Vecindades en dos dimensiones
Chaté-Manneville [4] hacen un análisis a través de la teoría de mean field, el mapa de retorno, series de tiempo, diagrama de evoluciones y el diagrama de bifurcaciones para poder explicar los comportamientos colectivos [5] y los comportamientos colectivos no triviales [6]. Cabe recalcar que el diagrama de bifurcaciones es muy útil para el modelo de lattices acopladas, donde la regla de evolución no está determinada de forma determinística, más bien de forma probabilística. Aclaramos que en este reporte sólo se trata el modelo determinístico.