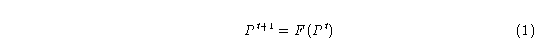
El cálculo de probabilidades en autómatas celulares ha sido un tema de considerable atención. Las funciones de probabilidad que representan la regla de evolución fueron aplicadas por Dresden y Wong [3] en 1975; y una manera para calcular la probabilidad fue propuesta por Schulman y Seiden [7], en 1978. Procedimientos más sofisticados como el cálculo de la probabilidad de un bloque tratado por Lipman y Shamma [8] y la generalización presentada en la teoría de la estructura local de Gutowitz [4] [5] [6], fueron de las últimas contribuciones al área.
La teoría del campo promedio es una de las técnicas presentadas en estos trabajos y es parte de la herencia de la mecánica estadística. La idea básica es que dado que no es posible estimar con precisión el comportamiento de un autómata celular, se propone predecir información más general como el promedio de células.
La aproximación mediante el campo promedio realiza lo anterior con la ventaja de sintetizar la composición de funciones de un autómata celular al cálculo iterativo de una función de una sola variable.
Donde P^(t+1) es la probabilidad (densidad) de aparición de un estado en el instante t+1 y F es la función que determina ese nuevo valor teniendo como argumento la densidad actual.
Varios autores han evaluado la precisión de la aproximación del campo promedio, Gutowitz en su tesis doctoral [4] realiza un análisis sobre varios autómatas celulares y muestra el nivel de divergencia entre el método y la evolución real del autómata. Chaté y Manneville también llevaron a cabo un análisis de evaluación en altas dimensiones, en donde encontraron el fenómeno conocido ahora como comportamiento colectivo no trivial [2] y el cual según los autores contradecía las predicciones de la teoría del campo promedio.
Aquí se muestran autómatas celulares binarios en tres, cuatro, cinco y seis dimensiones que reproducen el fenómeno de Chaté y Manneville y la aproximación del campo promedio en ellos.
Se compara la función compuesta del autómata celular con la función de iteración sobre la aproximación del campo promedio; la idea de esta comparación es ver que tanto se aproxima la teoría del campo promedio en la predicción de las densidades de período tres y cuasiperíodo tres encontradas por Chaté y Manneville.
Además se analiza si el traslape de las vecindades tiene relación con la dimensión del espacio y con la aproximación del campo promedio.