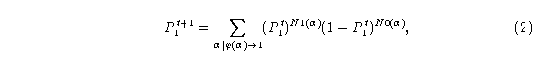
La deducción del cálculo de la probabilidad a partir del campo promedio, tiene un principio sencillo y elegante. Si se desea calcular la probabilidad de que aparezca un 1 en un autómata binario en la siguiente generación, debemos de calcular la probabilidad de que ocurran las cadenas ancestras que producen 1's.
Estos ancestros son los argumentos de la regla de evolución que determinan la asignación al estado 1, (es decir las vecindades) por lo que la probabilidad de que aparezca el estado 1 va a estar dada por la suma de las probabilidades de que ocurran las vecindades que lo originan. Y la probabilidad de que las vecindades ancestras ocurran está dada por la probabilidad de que aparezcan los estados que forman dichas vecindades o contraimágenes. De esta manera se puede definir recursivamente:
donde:
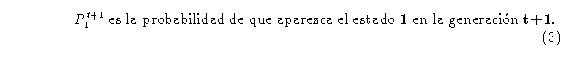
![]()
![]()
![]()

Sin embargo la aproximación del campo promedio adolece de un problema: asume que no existe correlación entre los estados de las células del autómata celular. Este supuesto no es exacto, ya que una de las características de un autómata celular es precisamente el traslape entre las células de sus vecindades y por lo tanto existe dependencia entre los estados de las células como lo ilustra la figura 1.
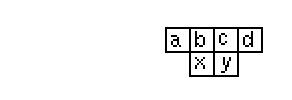
Figura 1: La probabilidad de que ocurra el estado y no es independiente del estado x ya que ambos comparten parte de los ancestros que los originan, por lo que el hecho de que aparezca y se debe de alguna manera al hecho de que haya ocurrido x.
Este hecho parece ser la causa de la divergencia entre la aproximación del campo promedio y la evolución real del autómata.