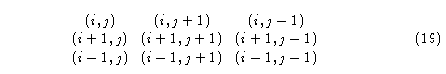
La vecindad de Moore en el plano está definida como una vecindad de nueve células:
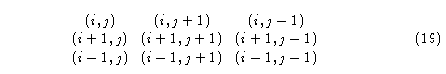
La vecindad de la célula (i+1,j) se traslapa con la vecindad de (i,j) en las células
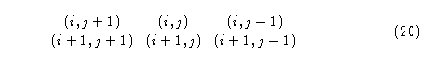
tomando como referencia a la primera vecindad, lo cual da un traslape de 2/3 (ver figura 3).
La vecindad de Moore en tres dimensiones está compuesta de 27 células, a saber:
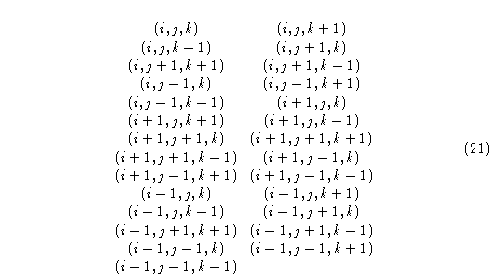
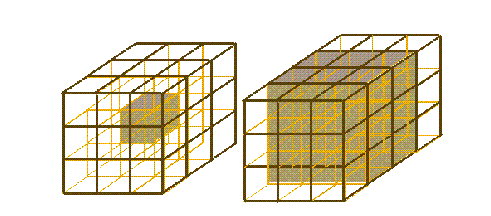
Figure 4: Vecindad de Moore y su traslape ortogonal en tres dimensiones.
El traslape de su vecino ortogonal es de un total de 18 células:
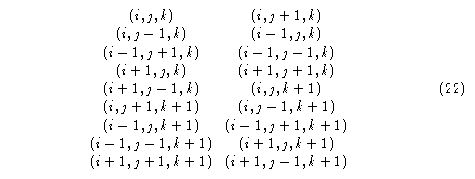
de las 27 que contiene la vecindad. De esta manera se tiene que 2/3 resulta ser el traslape en 3 dimensiones (ver fig 4).
En general la vecindad de Moore está definida por todas las posibilidades de tener una célula en el centro, y una célula desplazada un sitio en cualquier dirección. Esto se expresa en términos de coordenadas bajo tres formas:
![]()
En el plano esto significa tomar en cuenta las células de arriba y abajo, para un desplazamiento de tres posiciones sobre la recta, lo cual produce un total de 3x3=9 células, que puede expresarse como:
![]()
En tres dimensiones se tiene
![]()
3x3x3=27 y para cuatro dimensiones la vecindad tiene 81 células.
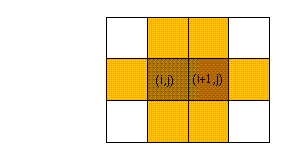
Figure 5: Traslape de la vecindad de von Neumann en dos dimensiones.
Por otro lado el traslape ortogonal de las vecindades está definido por la suma de las células de 2 subespacios de n-1 dimensiones sobre un espacio de n dimensiones:
![]()
De manera que el traslape en n=2 (el plano) es de 31+31=6, lo cual dividido entre el total de células de la vecindad nos da: 2/3. El traslape en 3 dimensiones es de
![]()
En general, como se mencionó el traslape en n dimensiones es
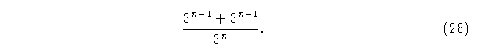
Desarrollando obtenemos el siguiente resultado:
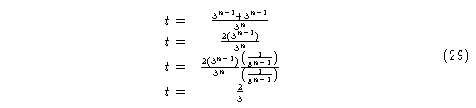
En conclusión, para la dimensión n el translape de las vecindades de Moore siempre será de 2/3
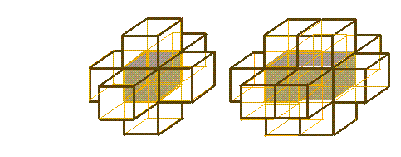
Figura 6: Vecindad de von Neumann en tres dimensiones y su traslape.