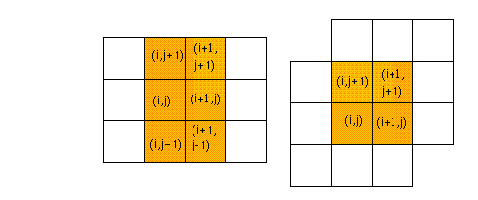
Figura 3: traslape en una vecindad de Moore en 2 dimensiones, tomando en cuenta vecindades de la célula vecina ortogonal y diagonal.
Chaté y Manneville han argumentado que la aproximación del campo promedio llega a ser más exacta a medida que aumenta la dimensión del espacio del autómata celular, concretamente cuando el límite del tamaño del espacio del autómata celular tiende a infinito [1]. Una razón que puede apoyar esta afirmación, es el hecho de que el traslape de las vecindades disminuye a medida que aumenta la dimensión y esto baje a su vez la correlación entre las células.
Aquí se analiza cómo se comporta el traslape de las vecindades en n dimensiones para la vecindad de von Neumann y Moore (ver figura 2)
, y se demuestra que en el caso de la vecindad de Moore no importa la dimensión del espacio, el traslape siempre será de 2/3. Sin embargo, el traslape en la vecindad de von Neumann sí depende de la dimensión del espacio, ya que disminuye a medida en que la dimensión aumenta; o en otros términos tiende a 0 cuando n tiende a infinito.
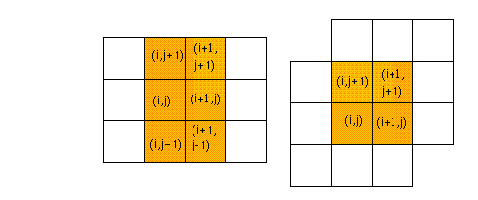
Figura 3: traslape en una vecindad de Moore en 2 dimensiones, tomando en cuenta vecindades de la célula vecina ortogonal y diagonal.