Sea 
Z y 
entonces 
es llamado un mapeo global [16] inducido por un mapeo local 
desde un punto de vista m. Un mapeo 
es llamado global si 
para alguna 
Z. Y sea f un
mapeo global de 
. Si 
es definido como 
para toda 
, entonces 
es llamado un mapeo global finito de 
.
Sea x una cadena entonces lg(x) denota la longitud de x. Sea 
una secuencia de longitud cero
y además es un cadena. Entonces para alguna 
, denotamos a 
una configuración finita de 
tal que si 
entonces 
por lo tanto 
para todo i
< 0 y para todo 
lg(x). Pero si 
entonces 
Z.
Decimos que un mapeo local induce un mapeo global por que el mapeo global conserva
todas las propiedades locales a través de todas las configuraciones. Estas propiedades
globales representadas por 
son las que determinan el comportamiento del mapeo global a través del tiempo.
Desarrollando de una manera más explicita ejemplificaremos las definiciones de los
párrafos anteriores sobre un autómata binario.
Como definimos en la Sección 3.2, 
representa los mapeos locales de una regla en particular. Entonces para una 
sobre una configuración 
denotamos un mapeo global
desde un punto de vista m y una posición i denotado por,
Si k = 2 y r = 1 entonces n = 3. Si i = 0 y m = 0
entonces el mapeo global 
se representa como:
por lo que se deduce que 
, entonces la condición i < 0 e 
lg(x) determina los límites de lg(x)
dentro una configuración 
.
Si i = 0 y m = -1 entonces el mapeo global 
se representa como:
podemos apreciar que el subíndice i indica la posición que ocupan cada una de
las configuraciones 
dentro
de la cadena x; m indica el punto de vista donde se localizan estas cadenas.
Las condiciones esTablacidas por i denotan un mapeo global finito de 
denotado por 
.
Si 
representa el mapeo
de las configuraciones finitas del conjunto 
entonces lg(x) es igual a l, donde 
P y denota el tamaño
de cualquier configuración 
.
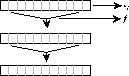
Figura 3.5: Mapeo global del conjunto 
.
Por lo que concluimos que 
para un mapeo global finito. Nótese que se emplea la notación original [16] 
con la notación propuesta en este escrito 
, donde la finalidad es la misma pero tratando de
especificar con mayor detalle los elementos que pertenecen al conjunto 
.
Finalmente desarrollamos el mapeo global para configuraciones no finitas. Para un mapeo
global de una configuración 
la correspondencia esta dada por las configuraciones mismas como elementos
del conjunto 
. El mapeo
global 
es el mapeo de
las mismas configuraciones de 
.
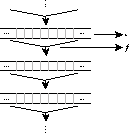
Figura 3.6: Mapeo global del conjunto 
.
Por lo tanto 
denota un
mapeo global por que las propiedades locales esTablacidas por 
y la localización de estas configuraciones
denotadas por m, son las mismas para toda configuración 
.